Nội Dung Chính
(Trang 111)
CHƯƠNG VIII. ĐIỆN TỬ SỐ
• Tín hiệu số và các cổng logic cơ bản
• Một số mạch xử lí tín hiệu trong điện tử số
• Thực hành: Lắp ráp, kiểm tra mạch báo cháy sử dụng các cổng logic cơ bản
(Trang 112)
BÀI 21. TÍN HIỆU SỐ VÀ CÁC CỔNG LOGIC CƠ BẢN
Sau khi học xong bài này, em sẽ:
Vẽ được kí hiệu, trình bày được công dụng và nhận biết được một số cổng logic cơ bản.
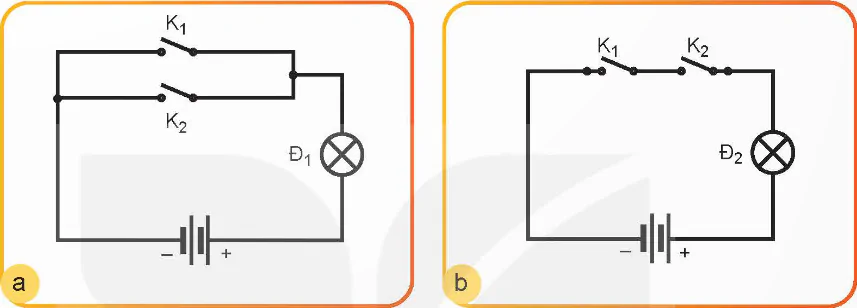
Hình 21.1
Quan sát Hình 21.1 và lập bảng các trạng thái đèn Đ1 và Đ2 (sáng/tối) khi các khóa K1 và K2 đóng/mở.
I. TÍN HIỆU SỐ VÀ CÁC THAM SỐ ĐẶC TRƯNG
1. Khái niệm tín hiệu số
Tín hiệu số là một chuỗi các tín hiệu rời rạc, có biên độ không đổi trong một khoảng thời gian nhất định (Hình 21.2).
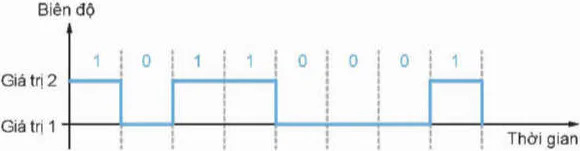
Hình 21.2. Tín hiệu số
Tín hiệu số có đặc điểm: Ít bị ảnh hưởng bởi nhiễu, dễ dàng khôi phục bằng cách sử dụng bộ lặp hoặc các bộ khuếch đại. Tín hiệu số được sử dụng phổ biến trong máy tính và các thiết bị kĩ thuật số, cho phép nhiều người dùng đồng thời, có thể nén, xử lí, mã hoá và bảo mật tốt hơn tín hiệu tương tự.
(Trang 113)
2. Các tham số đặc trưng của tín hiệu số
a) Bit và mức điện áp
Trong tín hiệu số, bit (0 hoặc 1) thường được biểu diễn bằng một mức điện áp (ví dụ mức thấp 0 V cho bit 0 và mức cao 5 V cho bit 1).
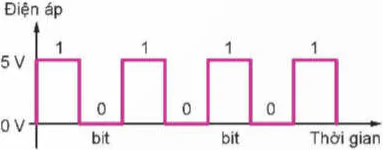
Hình 21.3. Bit và mức điện áp biểu diễn cho bit
b) Tốc độ bit và khoảng bit
Tốc độ bit là số bit trên 1 giây, kí hiệu là R, đơn vị là bit/giây (bit/s).
Khoảng bit (nghịch đảo của tốc độ bit) là thời gian kéo dài của một bit, kí hiệu là Tb, được tính theo công thức: 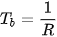 , đơn vị là giây.
, đơn vị là giây.
Hình 21.4 trình bày tốc độ bit và khoảng bit của một tín hiệu số.
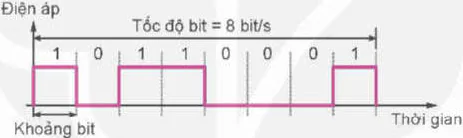
Hình 21.4. Tốc độ bit và khoảng bit
II. KHÁI NIỆM CỔNG LOGIC
Khám phá
Trong Hình 21.1, nếu quy ước trạng thái của các khoá K khi đóng là 1 và khi ngắt là 0; trạng thái của bóng đèn khi sáng là 1 và khi tắt là 0. Hãy hoàn thiện trạng thái của bóng đèn Đ₁ và Đ₂ tuỳ theo trạng thái của các khoá K trong hai bảng sau:
Bảng 21.1. K1 và K2 mắc song song
K1 K2 Đ1 0 0 ? 0 1 ? 1 0 ? 1 1 ? Bảng 21.2. K1 và K2 mắc nội tiếp
K1 K2 Đ1 0 0 ? 0 1 ? 1 0 ? 1 1 ?
Cổng logic là một mạch điện thực hiện chức năng của một hàm logic (hàm Boole). Mỗi cổng logic thực hiện một phép toán đại số logic trên một hoặc nhiều lối vào để tạo ra một kết quả logic duy nhất ở đầu ra.
(Trang 114)
i+ Thông tin bổ sung
- Đại số logic được nhà toán học người Anh George Boole đề xuất vào năm 1847, đây là công cụ toán học được dùng trong hệ thống đếm nhị phân.
- Với đại số logic, các hàm và các biến chỉ nhận một trong hai giá trị 0 hoặc 1. Hai giá trị này biểu diễn hai trạng thái logic đúng hoặc sai, điện áp cao (VH) hoặc thấp (VL), công tắc đóng hoặc ngắt, có hoặc không có dòng điện chạy trong mạch,...
- Đại số logic có ba phép toán cơ bản là phép cộng logic, phép nhân logic và phép phủ định.
- Bảng chân lí: là bảng mô tả quan hệ giữa biến logic đầu ra với các biến logic đầu vào theo một hàm logic nào đó.
Hình 21.5. George Boole (1815 - 1864)
III. MỘT SỐ CỔNG LOGIC CƠ BẢN
1. Cổng OR
- Hàm logic: y = x1 + x2
- Kí hiệu logic (Hình 21.6):

Hình 21.6. Kí hiệu cổng OR
Bảng 21.3. Bảng chân lí của cổng OR
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Khi ít nhất một trong hai lối vào x1 và x2 bằng 1 thì lối ra y bằng 1. Còn khi cả hai lối vào bằng 0 thì lối ra bằng 0. Trên thực tế, khi chế tạo các cổng OR, người ta tích hợp nhiều cổng trên một IC. Ví dụ IC 74LS32 có 4 cổng OR (Hình 21.7).

Hình 21.7. Sơ đồ chân và IC tích hợp 4 cổng OR (IC 74LS32)
Luyện tập
Vẽ sơ đồ logic của hàm y = (x1 + x2) + x3 sử dụng kí hiệu logic trong Hình 21.6.
Công dụng của cổng OR: Cổng OR được sử dụng trong việc cộng logic hai hoặc nhiều tín hiệu đầu vào thành một tín hiệu đầu ra và tạo ra kết quả logic phức tạp từ các tín hiệu đơn giản như mạch cộng tín hiệu, mạch điều khiển đóng ngắt,.…
(Trang 115)
2. Cổng AND
- Hàm logic: y = x1.x2
- Kí hiệu logic (Hình 21.8):
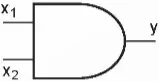
Hình 21.8. Kí hiệu cổng AND
Bảng 21.4. Bảng chân lí của cổng AND
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Khi cả hai lối vào x1 và x2 bằng 1 thì lối ra bằng 1. Còn khi ít nhất một trong hai lối vào bằng 0 thì lối ra bằng 0. Trên thực tế, khi chế tạo các cổng AND, người ta tích hợp nhiều cổng trên một IC. Ví dụ IC 74LS08 có 4 cổng AND (Hình 21.9).
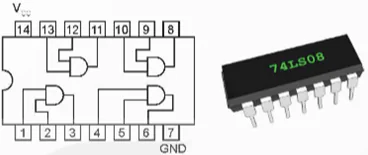
Hình 21.9. Sơ đồ chân và IC tích hợp 4 cổng AND (IC 74LS08)
Công dụng của cổng AND: Cổng AND được sử dụng trong việc nhân logic hai hoặc nhiều tín hiệu đầu vào thành một tín hiệu đầu ra và tạo ra kết quả logic phức tạp từ các tín hiệu đơn giản như mạch nhân tín hiệu, mạch điều khiển đóng/ngắt.
3. Cổng NOT
- Hàm logic: 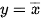
- Kí hiệu logic (Hình 21.10):
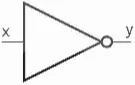
Hình 21.10. Kí hiệu cổng NOT
Bảng 21.5. Bảng chân lí của cổng NOT
| x | 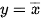 |
| 0 | 1 |
| 1 | 0 |
Lối ra y luôn có trạng thái ngược (đảo) với lối vào x. Trên thực tế, khi chế tạo các cổng NOT, người ta tích hợp nhiều cổng trên một IC. Ví dụ IC 74LS04 có 6 cổng NOT (Hình 21.11).

Hình 21.11. Sơ đồ chân và IC tích hợp 6 cổng NOT (IC 74LS04)
Công dụng của cổng NOT: Cổng NOT thường được sử dụng để đảo ngược trạng thái tín hiệu đầu vào hoặc điều khiển các tín hiệu logic trong mạch điện tử, mạch cảm biến,...
(Trang 116)
4. Cổng NOR
- Hàm logic: 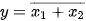
- Kí hiệu logic (Hình 21.12):
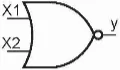
Hình 21.12. Kí hiệu cổng NOR
Bảng 21.6. Bảng chân lí của cổng NOR
| x1 | x2 | y |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
Cổng NOR có thể được thiết lập bằng cách mắc nối tiếp một cổng OR với một cổng NOT (Hình 21.13).
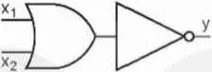
Hình 21.3. Cấu tạo cổng NOR từ OR và NOT
Khi ít nhất một trong hai lối vào x1 và x2 bằng 1 thì lối ra y bằng 0. Còn khi cả hai lối vào bằng 0 thì lối ra bằng 1. Trên thực tế, khi chế tạo các cổng NOR, người ta tích hợp nhiều cổng trên một IC. Ví dụ IC 74LS02 có 4 cổng NOR (Hình 21.14).
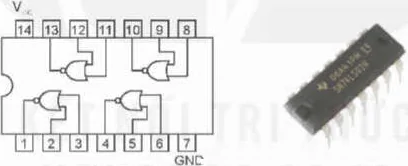
Hình 21.14. Sơ đồ chân và IC tích hợp 4 cổng NOR (IC 74LS02)
Công dụng của cổng NOR: Cổng NOR được sử dụng để đảo ngược trạng thái của mạch cộng logic hoặc điều khiển các tín hiệu logic trong mạch điện tử, mạch cảm biến,...
5. Cổng NAND
- Hàm logic: 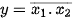
- Kí hiệu logic (Hình 21.15):
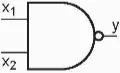
Hình 21.15. Kí hiệu cổng NAND
Bảng 21.7. Bảng chân lí của cổng NAND
| x1 | x2 | y |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
(Trang 117)
Cổng NAND có thể được tạo ra bằng cách mắc nối tiếp một cổng AND với một cổng NOT (Hình 21.16).
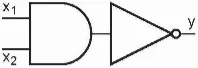
Hình 21.16. Cấu tạo cổng NAND từ AND và NOT
Khi cả hai lối vào x1 và x2 bằng 1 thì lối ra bằng 0. Còn khi ít nhất một trong hai lối vào bằng 0 thì lối ra bằng 1. Trên thực tế, khi chế tạo các cổng NAND, người ta tích hợp nhiều cổng trên một IC. Ví dụ IC 74LS00 có 4 cổng NAND (Hình 21.17).

Hình 21.17. Sơ đồ chân và IC tích hợp 4 cổng NAND (IC 74LS00)
Công dụng của cổng NAND: Cổng NAND được sử dụng để đảo ngược trạng thái của mạch nhân logic hoặc điều khiển các tín hiệu logic trong mạch điện tử, mạch cảm biến,...
Luyện tập
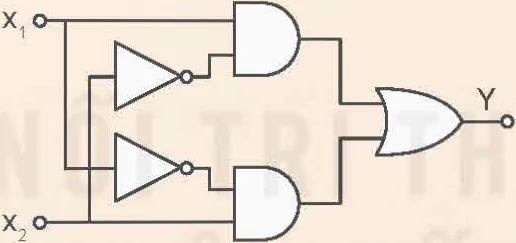
1. Quan sát Hình 21.18, viết hàm logic và bảng chân lí của hàm Y theo x1 và x2.
Hình 21.18. Sơ đồ hàm logic Y
2. Cho hàm logic
hãy vẽ sơ đồ của hàm logic này sử dụng các cổng logic cơ bản đã học ở trên.
Vận dụng
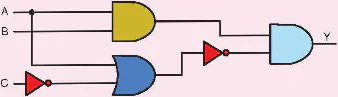
Cho sơ đồ của hàm logic Y như Hình 21.19. Hãy xác định trạng thái lối ra của Y theo các lối vào A, B, C cho trong bảng dưới đây:
Lối vào Lối ra A B C Y 0 0 0 ? 1 1 1 ?
Hình 21.19. Sơ đồ logic của hàm Y









































































Bình Luận
Để Lại Bình Luận Của Bạn