Trang 4
Trong chương này, luỹ thừa với số mũ nguyên được mở rộng cho số mũ hữu tỉ, số mũ thực và từ đó hình thành khái niệm lôgarit. Đây là những phép tính được sử dụng nhiều trong khoa học, kĩ thuật và đời sống. Trên cơ sở đó, hai hàm số quan trọng là hàm số mũ và hàm số lôgarit được giới thiệu. Phần cuối chương trình bày cách giải một số phương trình, bất phương trình mũ và lôgarit đơn giản.
| THUẬT NGỮ • Cơ số • Căn bậc n • Luỹ thừa với số mũ nguyên • Luỹ thừa với số mũ hữu tỉ • Luỹ thừa với số mũ thực • Số mũ | KIẾN THỨC, KĨ NĂNG • Nhận biết khái niệm luỹ thừa với số mũ nguyên của một số thực khác 0; luỹ thừa với số mũ hữu tỉ và luỹ thừa với số mũ thực của một số dương. • Giải thích các tính chất của lũy thừa với số mũ nguyên, luỹ thừa với số mũ hữu tỉ và lũy thừa với hữu luỹ thừa với thực. • Sử dụng tính chất của phép tính luỹ thừa trong tính toán các biểu thức số và rút gọn các biểu thức chứa biển. • Tính giá trị biểu thức số có chứa phép tính luỹ thừa bằng cách sử dụng máy tính cầm tay. • Giải quyết một số vấn đề có liên quan đến môn học khác hoặc thực tiễn gắn với phép tính luỹ thừa. |
Ngân hàng thường tính lãi suất cho khách hàng theo thể thức lãi kép theo định kì, tức là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp. Nếu một người gửi số tiền P với lãi suất r mỗi kì thì sau N k số tiền người đó thu được (cả vốn lẫn lãi) được tính theo công thức lãi kép sau:
A = P (1 + r)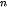

Trang 5
Bác Minh gửi tiết kiệm số tiền 100 triệu đồng kì hạn 12 tháng với lãi suất 6% một năm. Giả sử lãi suất không thay đổi. Tinh số tiền (cả vốn lẫn lãi) bác Minh thu được sau 3 năm.
1. LUỸ THỪA VỚI SỐ MŨ NGUYÊN
HĐ1. Nhận biết luỹ thừa với số mũ nguyên
Tính: (1,5)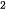 ;
; 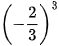 ;
; 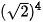 .
.
| • Cho n là một số nguyên dương. Ta định nghĩa: Với a là số thực tuỳ ý: 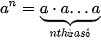 Với a là số thực khác 0: 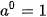 , , 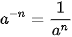 . .• Trong biểu thức 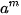 , a gọi là cơ số, m gọi là số mũ. , a gọi là cơ số, m gọi là số mũ. |

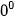
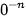 (n ∈ N*) không có nghĩa.
(n ∈ N*) không có nghĩa. Luỹ thừa với số mũ nguyên có các tính chất tương tự như luỹ thừa với số mũ nguyên dương.
Với a ≠ 0, b ≠ 0 và m, n là các số nguyên, ta có: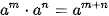 ; ;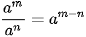 ; ;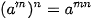 ; ;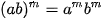 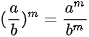 . . |
Chú ý
• Nếu a >1 thì 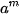 >
> 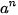 khi và chỉ khi m > n.
khi và chỉ khi m > n.
• Nếu 0 < a <1 thì 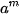 >
> 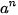
Ví dụ 1. Tính giá trị của biểu thức:
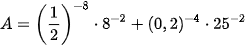
Giải
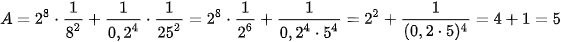 .
.
Luyện tập 1. Một số dương x được gọi là viết dưới dạng kí hiệu khoa học nếu x = a - 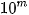 , ở đó 1 ≤ a < 10 và m là một số nguyên. Hãy viết các số liệu sau dưới dạng kí hiệu khoa học.
, ở đó 1 ≤ a < 10 và m là một số nguyên. Hãy viết các số liệu sau dưới dạng kí hiệu khoa học.
a) Khối lượng của Trái Đất khoảng 5 980 000 000 000 000 000 000 000 kg;
b) Khối lượng của hạt proton khoảng 0,000 000 000 000 000 000 000 000 001 67262 kg.
(Theo SGK Vật lí 12, Nhà Xuất bản Giáo dục Việt Nam, 2020)
Trang 6
2. LUỸ THỪA VỚI SỐ MŨ HỮU TỈ
HĐ2. Nhận biết khái niệm căn bậc n
a) Tìm tất cả các số thực x sao cho 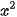 = 4.
= 4.
b) Tìm tất cả các số thực x sao cho 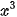
Cho số thực a và số nguyên dương n. Số b được gọi là căn bậc n của số a nếu 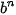 = a. = a. |
Nhận xét. Khi n là số lẻ, mỗi số thực a chỉ có một căn bậc n và kí hiệu là 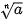 . Căn bậc 1 của số a chính là a.
. Căn bậc 1 của số a chính là a.
Khi n là số chẵn, mỗi số thực dương có đúng hai căn bậc n là hai số đối nhau, giá trị dương kí hiệu là 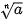 (gọi là căn số học bậc n của a), giá trị âm kí hiệu là –
(gọi là căn số học bậc n của a), giá trị âm kí hiệu là –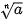 .
.

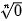 = 0 (n ∈ N*)
= 0 (n ∈ N*)
 Số âm có căn bậc chẵn không? Vì sao?
Số âm có căn bậc chẵn không? Vì sao?
Ví dụ 2. Tính:
a) 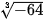 ;
;
b) 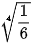 .
.
Giải
a) 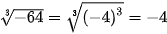
b) 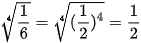
Luyện tập 2. Tính: a) 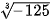 ; b)
; b) 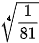 .
.
HĐ3. Nhận biết tính chất của căn bậc n
a) Tính và so sánh: 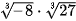 và
và 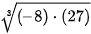
b) Tính và so sánh: 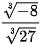 và
và 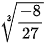
Giả sử n, k là các số nguyên dương, m là số nguyên. Khi đó: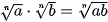 ; ;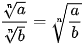 ; ;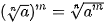 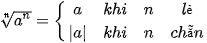 ; ;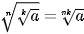 . .(Giả thiết các biểu thức ở trên đều có nghĩa). |
Trang 7
Ví dụ 3. Tính: a) 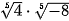 ; b)
; b)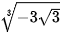 .
.
Giải
a) 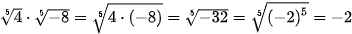
b) 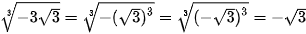 .
.
Luyện tập 3. Tính: a) 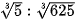 ; b)
; b) 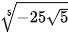 .
.
HĐ4. Nhận biết luỹ thừa với số mũ hữu tỉ
Cho a là một số thực dương.
a) Với n là số nguyên dương, hãy thử định nghĩa 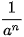 sao cho
sao cho 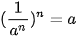
b) Từ kết quả của câu a, hãy thử định nghĩa 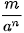 , với m là số nguyên và n là số nguyên dương, sao cho
, với m là số nguyên và n là số nguyên dương, sao cho 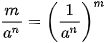 .
.

Lưu ý: 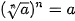 .
.
Cho số thực a dương và số hữu tỉ 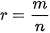 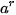 , xác định bởi , xác định bởi 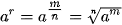 . . |
 Vì sao trong định nghĩa luỹ thừa với số mũ hữu tỉ lại cần điều kiện cơ số a > 0?
Vì sao trong định nghĩa luỹ thừa với số mũ hữu tỉ lại cần điều kiện cơ số a > 0?
Chú ý. Luỹ thừa với số mũ hữu tỉ (của một số thực dương) có đầy đủ các tính chất như luỹ thừa với số mũ nguyên đã nêu trong Mục 1.
Ví dụ 4. Tính: a) 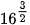 ; b)
; b) 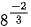
Giải
a) 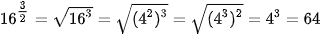 .
.
b) 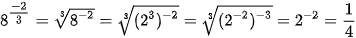 .
.
Luyện tập 4. Rút gọn biểu thức: 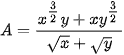 (x, y > 0)
(x, y > 0)
3. LUỸ THỪA VỚI SỐ MŨ THỰC
a) Khái niệm luỹ thừa với số mũ thực
HĐ5. Nhận biết luỹ thừa với số mũ thực
Ta biết rằng 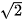 là một số vô tỉ và
là một số vô tỉ và 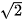
Gọi (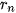 ) là dãy số hữu tỉ dùng để xấp xỉ số
) là dãy số hữu tỉ dùng để xấp xỉ số 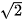 , với
, với 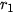 = 1;
= 1; 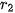 = 1.4;
= 1.4; 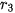
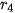 = 1,4142;...
= 1,4142;... 
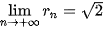
Trang 8
a) Dùng máy tính cầm tay, hãy tính: 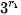 ;
; 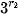
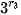 ;
; 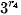 và
và 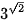 .
. b) Có nhận xét gì về sai số tuyệt đối giữa 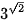 và
và 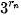
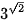 -
-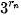 |, khi n càng lớn?
|, khi n càng lớn? Cho a là số thực dương và α là một số vô tỉ. Xét dãy số hữu tỉ (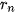 ) mà ) mà 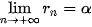 . Khi đó, dãy số ( . Khi đó, dãy số (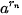 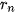 ) đã chọn. ) đã chọn.Giới hạn đó gọi là luỹ thừa của a với số mũ α, kí hiệu là 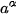 . .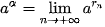 . . |
Chú ý. Luỹ thừa với số mũ thực (của một số dương) có đầy đủ các tính chất như luỹ thừa với số mũ nguyên đã nêu trong Mục 1.
Ví dụ 5. Rút gọn biểu thức: 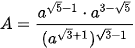 (a > 0)
(a > 0)
Giải
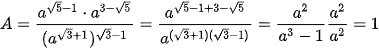
Ví dụ 6. Không sử dụng máy tính, hãy so sánh các số 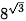 và
và 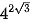 .
.
Giải
Ta có: 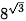 =
= 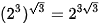 và
và 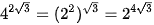
Vì 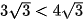 và 2 > 1 nên
và 2 > 1 nên 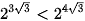 . Vậy
. Vậy 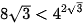 .
.

Ta đưa về so sánh hai luỹ thừa cùng cơ số.
Luyện tập 5. Rút gọn biểu thức: 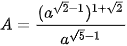
Vận dụng. Giải bài toán trong tình huống mở đầu.
b) Tính luỹ thừa với số mũ thực bằng máy tính cầm tay
Có thể sử dụng máy tính cầm tay để tính căn bậc n và luỹ thừa với số mũ thực.
| Tính (làm tròn kết quả đến chữ số thập phân thứ tư) | Bấm phím | Màn hình hiện | Kết quả |
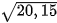 |  | 4.488875137 | 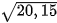 ≈ 4,4889 ≈ 4,4889 |
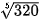 |  | 3.169786385 | 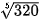 ≈3,1698 ≈3,1698 |
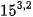 |  | 5800.855256 | 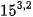 ≈ 5 800,8553 ≈ 5 800,8553 |
Trang 9
BÀI TẬP
6.1. Tính:
a) 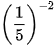
b) 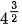 ;
;
c) 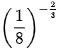 ;
;
d) 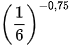 .
.
6.2. Thực hiện phép tính:
a)  ;
;
b) 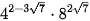
6.3. Rút gọn các biểu thức sau:
a) 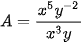 (x, y ≠ 0).
(x, y ≠ 0).
b) 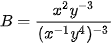 (x, y ≠ 0).
(x, y ≠ 0).
6.4. Cho x, y là các số thực dương. Rút gọn các biểu thức sau:
a) 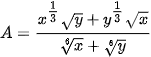 ;
;
b) 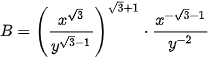
6.5. Chứng minh rằng: 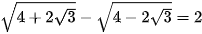
6.6. Không sử dụng máy tính cầm tay, hãy so sánh:
a) 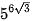 và
và 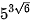 .
.
b) 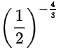 và
và 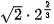 .
.
6.7. Nếu một khoản tiền gốc P được gửi ngân hàng với lãi suất hằng năm r (r được biểu thị dưới dạng số thập phân), được tính lãi n lần trong một năm, thì tổng số tiền A nhận được (cả vốn lẫn lãi) sau N kì gửi cho bởi công thức sau:
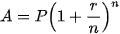
Hỏi nếu bác An gửi tiết kiệm số tiền theo triệu đồng theo kia han 6 tháng với lãi suất không đổi là 5% một năm, thì số tiền thu được (cả vốn lẫn lãi) của bác An sau 2 năm là bao nhiêu?
6.8. Năm 2021, dân số của một quốc gia ở châu Á là 19 triệu người. Người ta ước tính rằng dân số của quốc gia này sẽ tăng gấp đôi sau 30 năm nữa. Khi đó dân số A (triệu người) của quốc gia đó sau t năm kể từ năm 2021 được ước tính bằng công thức A = 19.230 Hỏi với tốc độ tăng dân số như vậy thì sau 20 năm nữa dân số của quốc gia này sẽ là bao nhiêu? (Làm tròn kết quả đến chữ số hàng triệu).









































































Bình Luận
Để Lại Bình Luận Của Bạn