Trang 95
| THUẬT NGỮ • Đạo hàm cấp hai • Gia tốc tức thời | KIẾN THỨC, KĨ NĂNG • Nhận biết khái niệm đạo hàm cấp hai của một hàm số. Tinh đạo hàm cấp hai của một số hàm số đơn giản. • Vận dụng đạo hàm cấp hai để giải quyết một số bài toán thực tiễn. |
Chuyển động của một vật gắn trên con lắc lò xo (khi bỏ qua ma sát và sức cản không khi) được cho bởi phương trình sau:
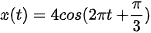
ở đó x tính bằng centimét và thời gian t tính bằng giây. Tìm gia tốc tức thời của vật tại thời điểm t = 5 giây (làm tròn kết quả đến hàng đơn vị).
Hình 9.9
1. KHÁI NIỆM ĐẠO HÀM CẤP HAI
HĐ1. Nhận biết đạo hàm cấp hai của một hàm số
a) Gọi g (x) là đạo hàm của hàm số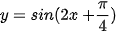 
. Tìm g (x)
b) Tính đạo hàm của hàm số y = g (x).
| Giả sử hàm số y = f (x) có đạo hàm tại mỗi điểm x ∈ (a; b). Nếu hàm số y' = f' (x) lại có đạo hàm tại x thì ta gọi đạo hàm của y' là đạo hàm cấp hai của hàm số y = f (x) tại x, kí hiệu là y" hoặc f" (x). |
Ví dụ 1. Tính đạo hàm cấp hai của hàm số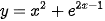 
. Từ đó tính y"(0).
Giải
Ta có: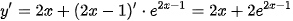 
;
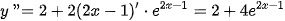
Vậy đạo hàm cấp hai của hàm số đã cho là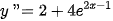 
.
Khi đó ta có: y"(0) = 2 + 4e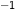
.
Luyện tập 1. Tính đạo hàm cấp hai của các hàm số sau:
a)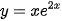 
;
b) y = In (2x + 3).
Trang 96
2. Ý NGHĨA CƠ HỌC CỦA ĐẠO HÀM CẤP HAI
Xét một chuyển động có vận tốc tức thời v (t). Cho số gia Δt tại t và Δv = v (t + Δt) - v (t). Tỉ số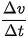 
gọi là gia tốc trung bình trong khoảng thời gian Δt. Giới hạn của gia tốc trung bình (nếu có) khi Δt dần tới 0 được gọi là gia tốc tức thời của chuyển động tại thời điểm t, kí hiệu là a (t). Như vậy
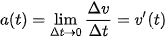
HĐ2. Nhận biết ý nghĩa cơ học của đạo hàm cấp hai
Xét một chuyển động có phương trình s = 4cos2πt.
a) Tìm vận tốc tức thời của chuyển động tại thời điểm t.
b) Tính gia tốc tức thời tại thời điểm t.
| Ý nghĩa cơ học của đạo hàm cấp hai Một chuyển động có phương trình s = f (t) thì đạo hàm cấp hai (nếu có) của hàm số f (t) là gia tốc tức thời của chuyển động. Ta có: a (t) = f" (t). |
Ví dụ 2. Giải bài toán trong tình huống mở đầu.
Giải
Vận tốc của vật tại thời điểm t là
.
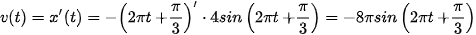Gia tốc tức thời của vật tại thời điểm t là
.
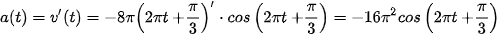Tại thời điểm t = 5, gia tốc của vật là
.
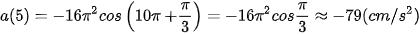Vận dụng. Một vật chuyển động thẳng có phương trình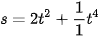 
(s tính bằng mét, t tính bằng giây). Tìm gia tốc của vật tại thời điểm t = 4 giây.
BÀI TẬP
9.13. Cho hàm số f (x) = x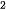
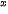. Tính f"(0) . 9.14. Tính đạo hàm cấp hai của các hàm số sau:
a) y = In (x + 1);
b) y = tan2x.
9.15. Cho hàm số P (x) = ax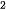 + bx + 3 (a, b là hằng số). Tìm a, b biết P' (1) = 0 và P"(1) = -2.
9.16. Cho hàm số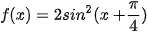 
. Chứng minh rằng |f" (x)| ≤ 4 với mọi x.
9.17. Phương trình chuyển động của một hạt được cho bởi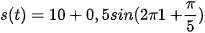 
, trong đó s tính bằng centimét và t tính bằng giây. Tính gia tốc của hạt tại thời điểm t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).
Các Bài Học Khác
Bình Luận
Để Lại Bình Luận Của Bạn