Một Vài Áp Dụng Của Toán Học Trong Tài Chính | Toán tập 1 | Hoạt Động Thực Hành Trải Nghiệm - Lớp 11 - Kết Nối Tri Thức Với Cuộc Sống

Trang 125

MỤC TIÊU

Học sinh biết vận dụng toán học để giải quyết một số vấn đề tài chính như bài toán gửi tiết kiệm tích luỹ, bài toán vay trả góp.

Chuẩn bị:

– Bảng lãi suất gửi tiết kiệm tích luỹ của một số ngân hàng;

– Bảng lãi suất vay trả góp (khi mua nhà, ô tô, ...) của một số ngân hàng,

– Máy tính cầm tay.

Thực hiện: Chia lớp làm bốn nhóm và tiến hành như sau: 

Bước 1. Các nhóm cùng thực hiện HĐ1, HĐ2, HĐ3 trong bài học, dưới sự hướng dẫn của giáo viên, để hiểu các khái niệm và công thức cần thiết.

Bước 2. Dựa vào dữ liệu đã có ở phần Chuẩn bị và gợi ý trong các Vận dụng trong bài học, GV đặt ra nhiệm vụ thực tế cụ thể cho từng nhóm. Mỗi nhóm sẽ thực hiện một nhiệm vụ riêng. Các nhóm hoàn thành nhiệm vụ được giao, sau đó báo cáo trước lớp.

Nhiều giao dịch tài chính như gửi tiết kiệm tích luỹ, vay trả góp,... liên quan đến các khoản thanh toàn được thực hiện đều đặn. Ví dụ, nếu gửi đều đặn 5 triệu đồng mỗi tháng vào một tài khoản tích luỹ có lãi suất 6% một năm, thì giá trị tài khoản của bạn sẽ là bao nhiêu vào cuối năm thứ 5? Nếu vay 1 tỉ đồng để mua nhà với lãi suất 9% một năm, thì số tiền bạn phải trả hằng tháng là bao nhiêu để có thể trả hết khoản vay này trong 10 năm?

Những câu hỏi như vậy liên quan đến tổng các số hạng của một dãy số. Trong bài này, chúng ta sẽ sử dụng kiến thức về công thức lãi kép và cấp số nhân để trả lời những câu hỏi này.

Trang 126

1. SỐ TIỀN CỦA MỘT NIÊN KIM

Niền kim là một khoản tiền được trả bằng các khoản thanh toán đều đặn. Mặc dù từ “niên kim" nghĩa là các khoản thanh toán hằng năm, thực tế chúng có thể được thực hiện thanh toán nữa năm, hằng quý, hằng tháng hoặc sau những khoảng thời gian đều đặn khác. Thanh toán thường được thực hiện vào cuối khoảng thời gian thanh toán. Số tiền của một niên kim là tổng của tất cả các khoản thanh toán riêng lẻ từ thời điểm thanh toán đầu tiên cho đến khi thanh toán cuối cùng được thực hiện, cùng với tất cả tiền lãi.

HĐ1. Số tiền của một niên kim

Bác Lan gửi đều đặn 10 triệu đồng vào ngày đầu mỗi tháng trong vòng 5 năm vào một tài khoản tích luỹ hưởng lãi suất 6% mỗi năm, theo hình thức tính lãi kép hằng tháng.

a) Tính số tiền có trong tài khoản vào cuối kì thứ nhất, cuối kì thứ hai.

b) Tính số tiền có trong tài khoản vào cuối kì thứ 1.

c) Tính số tiền có trong tài khoản ngay sau lần thanh toán cuối cùng.

Nói chung, khoản thanh toán theo niên kim được gọi là tiền thuê định kì và kí hiệu là R. Gọi i là lãi suất trong mỗi khoảng thời gian thanh toán và gọi n là số lần trả. Chúng ta luôn giả thiết rằng khoảng thời gian tính lãi kép bằng thời gian giữa các lần thanh toán. Bằng cách lập luận tương tự như trong HĐ1, chúng ta thấy rằng số tiền A, của một niền kim là

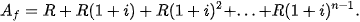
Vì đây là tổng của n số hạng đầu tiên của một cấp số nhân với số hạng đầu tiên a = R và công bội r = 1 + i, nên ta có

Số tiền của niên kim Số tiền 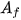 của một niên kim bao gồm n khoản thanh toán đều đặn bằng nhau và bằng R với lãi suất i trong mỗi khoảng thời gian được cho bởi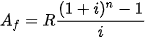

Vận dụng 1. Anh Binh cần đầu tư bao nhiêu tiền hằng tháng với lãi suất 9% mỗi năm, theo hình thức tính lãi kép hằng tháng, để có 200 triệu đồng sau hai năm?

2. GIÁ TRỊ HIỆN TẠI CỦA MỘT NIÊN KIM

Nếu bạn nhận được 100 triệu đồng trong vòng 5 năm kể từ bây giờ, nó sẽ có giá trị thấp hơn nhiều so với việc nếu bạn nhận được 100 triệu đồng ngay bây giờ. Điều này là do số tiền lãi mà bạn có thể tích lũy trong 5 năm tới nếu bạn đầu tư số tiền đó ngay bây giờ. Bạn sẽ chấp nhận số tiền nhỏ hơn nào bây giờ thay vì việc nhận 100 triệu đồng trong 5 năm tới? Đây là số tiền, cùng với tiền lãi, sẽ trị giá 100 triệu đồng trong 5 năm tới. Số tiền này được gọi là giá trị hiện tại.

HĐ2. Nhận biết giá trị hiện tại của một số tiền

Giả sử một người gửi tiết kiệm với lãi suất không đổi 6% một năm, theo hình thức tính lãi kép hằng quý.

a) Tính lãi suất i trong mỗi quý và số khoảng thời gian tính lãi trong vòng 5 năm.

Trang 127

b) Giả sử sau 5 năm người đó nhận được số tiền 100 triệu đồng cả vốn lẫn lãi. Tinh giá trị hiện tại của số tiền 100 triệu đồng đó.

Tương tự, nếu số tiền 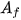được trả dần trong n khoảng thời gian kể từ bây giờ và lãi suất trong mỗi khoảng thời gian là i, thì giá trị hiện tại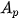

.

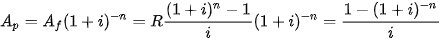Giá trị hiện tại của một niên kim Giá trị hiện tại của một niên kim bao gồm n khoản thanh toán đều đặn bằng nhau và bằng R với lãi suất i trong mỗi khoảng thời gian được cho bởi .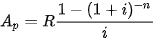

Vận dụng 2. Một người trúng xổ số giải đặc biệt với trị giá 5 tỉ đồng và số tiền trúng thưởng sẽ được trả dần hằng năm, mỗi năm là 500 triệu đồng trong vòng 10 năm. Giá trị hiện tại của giải đặc biệt này là bao nhiêu? Giả sử rằng người đó có thể tìm được hình thức đầu tư với lãi suất 8% mỗi năm, tính lãi kép hằng năm.

3. MUA TRẢ GÓP

Khi bạn mua một căn nhà hoặc một chiếc xe ô tô theo hình thức trả góp, các khoản thanh toán mà bạn thực hiện là một khoản niên kim có giá trị hiện tại là số tiền của khoản vay.

HĐ3. Anh Hưng muốn mua một chiếc xe ô tô theo hình thức trả góp để chạy xe dịch vụ. Anh ấy có thể trả dần 10 triệu nêu đồng mỗi tháng nhưng không có tiền trả trước. Nếu anh Hưng có thể thực hiện các khoản thanh toán này trong vòng 5 năm và lãi suất là 10% một năm, thì hiện tại anh ấy có thể mua được chiếc xe ô tô với mức giá nào?

Trả góp là phương thức cho vay tiền mà các kì trả nợ gốc và lãi trùng nhau. Số tiền trả nợ của mỗi kì là bằng nhau theo thoả thuận và số lãi được tỉnh dựa trên số dư nợ gốc và thời hạn thực tế của ki hạn trả nợ. Trả góp còn áp dụng trong việc cho vay tiêu dùng, mua tài sản giá trị lớn như nhà đất,  ô tô, ...

Mua trả góp

Nếu một khoản vay 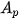phải được hoàn trả trong n lần thanh toán đều đặn bằng nhau với lãi suất i trong mỗi khoảng thời gian thì số tiền R của mỗi khoản thanh toán là .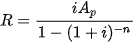

Vận dụng 3. Một cặp vợ chồng trẻ vay ngân hàng 1 tỉ đồng với lãi suất 9% một năm để mua nhà. Họ dự định sẽ trả góp hằng tháng trong vòng 10 năm để hoàn trả khoản vay này. Hỏi mỗi tháng họ sẽ phải trả cho ngân hàng bao nhiêu tiền?