Nội Dung Chính
Trang 62
| THUẬT NGỮ • Số trung bình • Trung vị • Tứ phân vị • Mót | KIẾN THỨC, KĨ NĂNG • Tính các số đặc trưng đo xu thế trung tâm của mẫu số liệu ghép nhóm. • Hiểu ý nghĩa, vai trò của các số đặc trưng của mẫu số liệu thực tế. |
Một cửa hàng đã ghi lại số tiền bán xăng cho 35 khách hàng đi xe máy. Mẫu số liệu gốc có dạng: 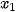
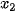 ,...,
,..., 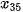 trong đó
trong đó 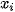 là số tiền bán xăng cho khách hàng thứ i. Vì một lí do nào đó, cửa hàng chỉ có mẫu số liệu ghép nhóm dạng sau:
là số tiền bán xăng cho khách hàng thứ i. Vì một lí do nào đó, cửa hàng chỉ có mẫu số liệu ghép nhóm dạng sau: | Số tiền (nghìn đồng) | [0;30) | [30; 60) | [60; 90) | [90; 120) |
| Số khách hàng | 3 | 15 | 10 | 7 |
Bảng 3.1. Số tiền khách hàng mua xăng
Dựa trên mẫu số liệu ghép nhóm này, làm thế nào để ước lượng các số đặc trưng đo xu thế trung tâm (số trung bình, trung vị, tử phân vị, mốt) cho mẫu số liệu gốc?
Chúng ta cũng tìm hiểu vấn đề này!
1. SỐ TRUNG BÌNH CỦA MẪU SỐ LIỆU GHÉP NHÓM
HĐ1. Khảo sát thời gian tự học của các học sinh trong lớp theo mẫu bên.
a) Hãy lập bảng thống kê cho mẫu số liệu ghép nhóm thu được.
b) Có thể tính chính xác thời gian tự học trung bình của các học sinh trong lớp không?
tự học của các học sinh trong lớp theo
c) Có cách nào tính gần đúng thời gian tự học trung bình của các học sinh trong lớp dựa trên mẫu số liệu ghép nhóm này không? Cho mẫu số liệu ghép nhóm
| Nhóm | [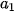 ; ; 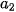 | ... | [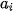 ; ; 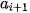 ) ) | [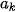 ; ; 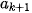 ) ) |
| Tần số | 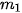 | ... | 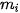 | 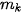 |
Bảng 3.2

Mỗi ngày em tự học trong bao nhiêu giờ ?
B. Từ 1,5 giờ đến dưới 3 giờ.
A. Dưới 1,5 giờ.
C.Từ 3 giờ đến dưới 4,5 giờ.
D.Từ 4,5 giờ trở lên.
Số trung bình của mẫu số liệu ghép nhóm kí hiệu là 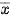 .
.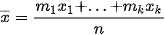
trong đó, n =
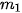 + ... +
+ ... + 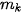 là cỡ mẫu và
là cỡ mẫu và 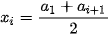
(với i = 1, ..., k) là giá trị đại diện của nhóm [
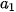 ;
; 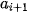
Trang 63
Chú ý. Đối với số liệu rời rạc, người ta thường cho các nhóm dưới dạng  , trong đó
, trong đó 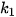 ,
, 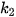 ∈ N. Nhóm K,- K, được hiểu là nhóm gồm các giá trị K, K, + 1, ..., kỵ. Khi đó, ta cần hiệu chỉnh mẫu dữ liệu ghép nhóm để đưa về dạng Bảng 3.2 trước khi thực hiện tính toán các số đặc trưng bằng cách hiệu chỉnh nhóm
∈ N. Nhóm K,- K, được hiểu là nhóm gồm các giá trị K, K, + 1, ..., kỵ. Khi đó, ta cần hiệu chỉnh mẫu dữ liệu ghép nhóm để đưa về dạng Bảng 3.2 trước khi thực hiện tính toán các số đặc trưng bằng cách hiệu chỉnh nhóm  với
với 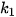
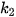 ∈ N thành nhóm [
∈ N thành nhóm [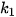 – 0,5;
– 0,5; 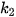 + 0,5). Chẳng hạn, với dữ liệu ghép nhóm điểm thi môn Toán trong Bảng 3.3 sau khi hiệu chỉnh ta được Bảng 3.4.
+ 0,5). Chẳng hạn, với dữ liệu ghép nhóm điểm thi môn Toán trong Bảng 3.3 sau khi hiệu chỉnh ta được Bảng 3.4. | Điểm thi | 1-4 | 5-7 | 8-10 |
| Số học sinh | 5 | 20 | 10 |
Bảng 3.3
| Điểm thi | [0,5; 4,5) | [4,5; 7,5) | [7,5; 10] |
| Số học sinh | 5 | 20 | 10 |
Bảng 3.4
Ví dụ 1. Tìm cân nặng trung bình của học sinh lớp 11D cho trong Bảng 3.5.
| Cân nặng | [40,5; 45,5) | [45,5; 50,5) | [50,5; 55,5) | [55,5; 60,5) | [60,5; 65,5) | [65,5; 70,5) |
| Số học sinh | 10 | 7 | 16 | 4 | 2 | 3 |
Bảng 3.5. Cân nặng của học sinh lớp 11D
Giải
Trong mỗi khoảng cân nặng, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có bảng sau:
| Cân nặng (kg) | 43 | 48 | 53 | 58 | 63 | 68 |
| Số học sinh | 10 | 7 | 16 | 4 | 2 | 3 |
Tổng số học sinh là n = 42. Cân nặng trung bình của học sinh lớp 11D là
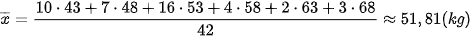 .
.
Luyện tập 1. Tìm hiểu thời thu được kết quả sau:
| Thời gian (giờ) | [0; 5) | [5:10) | [10:15) | [15:20) | [20; 25) |
| Số học sinh | 8 | 16 | 4 | 2 | 2 |
Tính thời gian xem ti vi trung bình trong tuần trước của các bạn học sinh này.
Ý nghĩa. Số trung bình của mẫu số liệu ghép nhóm xấp xỉ cho số trung bình của mẫu số liệu gốc, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.
2. TRUNG VỊ CỦA MẪU SỐ LIỆU GHÉP NHÓM
HĐ2. Cho mẫu số liệu ghép nhóm về chiều cao của 21 cây na giống.
| Chiều cao (cm) | [0; 5) | [5:10) | [10:15) | [15:20) |
| Số cây | 3 | 8 | 7 | 3 |
Gọi 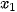
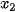 , ...,
, ..., 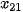 là chiều cao của các cây giống, đã được sắp xếp theo thứ tự tăng dần. Khi đó,
là chiều cao của các cây giống, đã được sắp xếp theo thứ tự tăng dần. Khi đó, 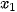 , ...,
, ..., 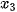 thuộc [0; 5),
thuộc [0; 5), 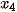
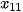 thuộc [5; 10), ... Hỏi trung vị thuộc nhóm nào?
thuộc [5; 10), ... Hỏi trung vị thuộc nhóm nào? Trang 64
Cho mẫu số liệu ghép nhóm như trong Bảng 3.2.
| Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau: Bước 1. Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ p: [ 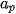 ; ; 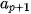 ). ).Bước 2. Trung vị là  , ,trong đó n là cỡ mẫu, 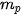 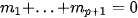 . . |
Ví dụ 2. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
| Thời gian (phút) | [9,5;12,5) | [12,5; 15,5) | [15,5; 18,5) | [18,5; 21,5) | [21,5; 24,5) |
| Số học sinh | 3 | 12 | 15 | 24 | 2 |
Tính trung vị của mẫu số liệu ghép nhóm này.
Giải
Cỡ mẫu là n = 3 + 12 +15+24 + 2 = 56.
Gọi 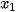 , ...,
, ..., 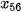 là thời gian vào Internet của 56 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là
là thời gian vào Internet của 56 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là  . Do 2 giá trị
. Do 2 giá trị 
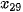 thuộc nhóm [15,5; 18,5) nên nhóm này chứa trung vị. Do đó, p = 3;
thuộc nhóm [15,5; 18,5) nên nhóm này chứa trung vị. Do đó, p = 3; 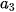 = 15,5;
= 15,5; 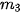 = 15;
= 15; 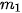 +
+ 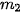
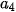 –
– 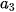 = 3 và ta có
= 3 và ta có 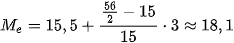 .
.
Luyện tập 2. Ghi lại tốc độ bỏng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết quả như bằng bên. Tính trung vị của mẫu số liệu ghép nhóm này.
| Tốc độ v (km/h) | Số lần |
| 150 ≤ v <155 | 18 |
| 155 ≤ v <160 | 28 |
| 160 ≤ v <165 | 35 |
| 165 < v <170 | 43 |
| 170 ≤ v < 175 | 41 |
| 175 ≤ v < 180 | 35 |
Ý nghĩa. Trung vị của mẫu số liệu ghép nhóm xấp xỉ cho trung vị của mẫu số liệu gốc, nó chia mẫu số liệu thành hai phần, mỗi phần chứa 50% giá trị.
3. TỨ PHÂN VỊ CỦA MẪU SỐ LIỆU GHÉP NHÓM
HĐ3. Với mẫu số liệu ghép nhóm cho trong HĐ2, hãy cho biết tứ phân vị thứ nhất 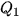 và tứ phân vị thứ ba
và tứ phân vị thứ ba 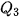
Cho mẫu số liệu ghép nhóm như Bảng 3.2.

Với tứ phân vị 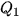 ,
, 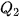 ,
, 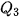 lần lượt có 25%, 50%, 75% số giá trị nhỏ hơn
lần lượt có 25%, 50%, 75% số giá trị nhỏ hơn 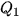
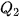 ,
, 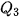 .
. Trang 65
Để tính tứ phân vị thứ nhất 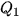 của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa 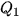 , giả sử đó là nhóm thử p: [ , giả sử đó là nhóm thử p: [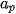 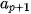 ). Khi đó, ). Khi đó,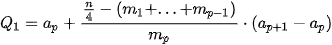 , ,trong đó, n là cỡ mẫu, 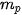 là tần số nhóm p, với p = 1 ta quy ước là tần số nhóm p, với p = 1 ta quy ước 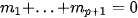 . .Để tính tứ phân vị thứ ba 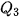 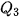 . Giả sử đó là nhóm thứ p: [ . Giả sử đó là nhóm thứ p: [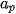 ; ; 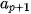 ). Khi đó, ). Khi đó,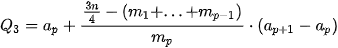 , ,trong đó, n là cỡ mẫu, 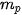 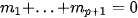 . .| Tứ phân vị thứ hai 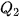 chính là trung vị chính là trung vị 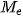 . . |
Ví dụ 3. Tìm tử phân vị thứ nhất 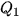 và tử phân vị thứ ba
và tử phân vị thứ ba 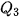
Giải
Cỡ mẫu là n = 56.
Tứ phân vị thứ nhất 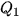 là
là 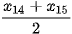 . Do
. Do 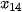 ,
, 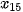 đều thuộc nhóm [12,5; 15,5) nên nhóm này chứa
đều thuộc nhóm [12,5; 15,5) nên nhóm này chứa 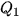
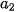 = 12,5;
= 12,5; 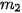 = 12;
= 12; 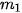 = 3,
= 3, 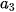 –
– 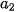
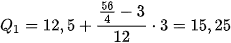 .
.
Với tứ phân vị thứ ba 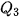 là
là 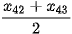 . Do
. Do 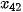 ,
, 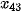
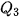 . Do đó, p = 4;
. Do đó, p = 4; 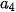 = 18,5;
= 18,5; 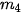 = 24;
= 24; 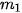 +
+ 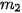
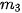 = 3 + 12 + 15 = 30;
= 3 + 12 + 15 = 30; 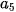 –
– 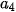 = 3 và ta có
= 3 và ta có 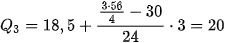 .
.
Nhận xét. Ta cũng có thể xác định nhóm chứa tứ phân vị thứ r nhờ tính chất có khoảng 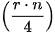
Luyện tập 3. Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba cho mẫu số liệu ghép nhóm ở Luyện tập 2.
Ý nghĩa. Các tử phân vị của mẫu số liệu ghép nhóm xấp xỉ cho các tử phân vị của mẫu số liệu gốc, chúng chia mẫu số liệu thành 4 phần, mỗi phần chứa 25% giá trị.
Trang 66
4. MỐT CỦA MẪU SỐ LIỆU GHÉP NHÓM
HĐ4. Với số liệu cho trong Luyện tập 1:
a) Có thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh không?
b) Mốt thuộc nhóm nào là hợp lí nhất? Nên lấy số nào trong nhóm để ước lượng cho mắt? Cho mẫu số liệu ghép nhóm như trong Bảng 3.2.
Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1. Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: [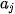 ;
; 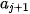 ).
).
Bước 2. Mốt được xác định là 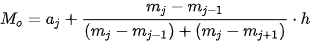
trong đó 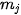 là tần số của nhóm j (quy ước
là tần số của nhóm j (quy ước 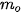
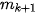 = 0) và h là độ dài của nhóm.
= 0) và h là độ dài của nhóm. Lưu ý. Người ta chỉ định nghĩa mốt cho mẫu ghép nhóm có độ dài các nhóm bằng nhau. Một mẫu có thể không có mắt hoặc có nhiều hơn một mốt.

Khi tần số của các nhóm số liệu bằng nhau thì mẫu số liệu ghép nhóm không có mốt.
Ví dụ 4. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A.
| Khoảng chiều cao (cm) | [145; 150) | [150; 155) | [155, 160) | [160; 165) | [165; 170) |
| Số học sinh | 7 | 14 | 10 | 10 | 9 |
Tính mốt của mẫu số liệu ghép nhóm này. Có thể kết luận gì từ giá trị tính được?
Giải
Tần số lớn nhất là 14 nên nhóm chứa mốt là nhóm [150; 155). Ta có, j = 2, 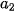 = 150,
= 150, 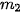 = 14,
= 14, 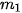
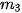 = 10, h = 5. Do đó
= 10, h = 5. Do đó 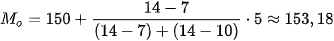 .
.
Số học sinh có chiều cao khoảng 153,18 cm là nhiều nhất.
Luyện tập 3. Thời gian (phút) để học sinh hoàn thành một câu hỏi thi được cho như sau:
| Thời gian (phút) | [0,5; 10,5) | [10,5; 20,5) | [20,5; 30,5) | [30,5; 40,5) | [40,5; 50,5) |
| Số học sinh | 2 | 10 | 6 | 4 | 3 |
Ý nghĩa. Mốt của mẫu số liệu ghép nhóm xấp xỉ cho một của mẫu số liệu gốc, nó được dùng để đo xu thế trung tâm của mẫu số liệu.
Vận dụng. Hãy tính các số đặc trưng cho mẫu số liệu trong Bảng 3.1 và giải thích ý nghĩa của các giá trị thu được.
Trang 67
BÀI TẬP
3.4. Quãng đường (km ) từ nhà đến nơi làm việc của 40 công nhân một nhà máy được ghi lại như sau:
5 3 10 20 25 11 13 7 12 31 19 10 12 17 18 11 32 17 16 2
7 9 7 8 3 5 12 15 18 3 12 14 2 9 6 15 15 7 6 12.
a) Ghép nhóm dãy số liệu trên thành các khoảng có độ rộng bằng nhau, khoảng đầu tiên là [0; 5). Tìm giá trị đại diện cho mỗi nhóm.
b) Tính số trung bình của mẫu số liệu không ghép nhóm và mẫu số liệu ghép nhóm. Giá trị nào chính xác hơn?
c) Xác định nhóm chứa mốt của mẫu số liệu ghép nhóm thu được.
3.5. Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho như sau:
| Tuổi thọ (năm) | [2; 2,5) | [2,5; 3) | [3: 3,5) | [3,5; 4) | [4: 4,5) | [4,5; 5) |
| Tần số | 4 | 9 | 14 | 11 | 7 | 5 |
a) Xác định mốt và giải thích ý nghĩa.
b) Tính tuổi thọ trung bình của 50 bình ắc quy ô tô này.
3.6. Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của 60 thí sinh được cho trong bảng sau:
| Điểm | 0-9 | 10-19 | 20-29 | 30-39 | 40-49 |
| Số thí sinh | 1 | 2 | 4 | 6 | 15 |
| Điểm | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
| Số thí sinh | 12 | 10 | 6 | 3 | 1 |
a) Hiệu chỉnh để thu được mẫu số liệu ghép nhóm dạng Bảng 3.2.
b) Tìm các tử phân vị và giải thích ý nghĩa của chúng.
3.7. Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối, thu được bảng số liệu ở bên.
a) So sánh thời gian ngủ trung bình của các bạn học sinh nam và nữ.
b) Hãy cho biết 75% học sinh khối 11 ngủ ít nhất bao nhiêu giờ?
| Thời gian | Số học sinh nam | Số học sinh nữ |
| [4; 5) | 6 | 4 |
| [5; 6) | 10 | 8 |
| [6; 7) | 13 | 10 |
| [7; 8) | 9 | 11 |
| [8; 9) | 7 | 8 |
Trang 68
Em có biết?
Ta có thể sử dụng phần mềm Geogebra để tính các tứ phân vị của mẫu số liệu ghép nhóm dạng Bảng 3.2 theo các bước sau đây:
Bước 1. Lập bảng tần số tích luỹ dạng sau:
| Nhóm | < 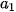 | [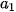 ; ; 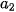 | ... | [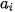 ; ; 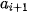 ) ) | ... | [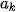 ; ; 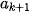 ] ] |
| Tần số tích luỹ | 0 | 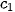 | ... | 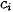 | ... | 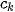 |
trong đó 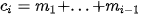 là tần số tích luỹ.
là tần số tích luỹ.
Bước 2. Vẽ đồ thị tần số tích luỹ bằng cách nối các điểm liên tiếp 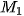 (
(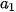
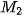 (
(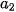 ;
; 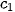 ), ...,
), ..., 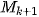 (
(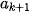
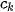 ).
). Bước 3. Qua điểm 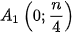 vẽ tia song song với Ox, cắt đồ thị tần số tích luỹ tại
vẽ tia song song với Ox, cắt đồ thị tần số tích luỹ tại 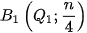 , với n là cỡ mẫu,
, với n là cỡ mẫu, 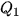 chính là tứ phân vị thứ nhất.
chính là tứ phân vị thứ nhất.
Qua điểm 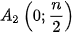
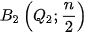 .
. 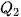 chính là tử phân vị thứ hai.
chính là tử phân vị thứ hai. Qua điểm 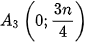 vẽ tia song song với Ox, cắt đồ thị tần số tích luỹ tại
vẽ tia song song với Ox, cắt đồ thị tần số tích luỹ tại 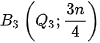 ,
, 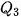
Chẳng hạn, với mẫu số liệu ghép nhóm cho trong Ví dụ 2 ta có bảng tần số tích luỹ:
| Nhóm | < 9,5 | [9,5; 12,5) | [12,5; 15,5) | [15,5; 18,5) | [18,5; 21,5) | [21,5; 24,5) |
| Tần số tích luỹ | 0 | 3 | 15 | 30 | 54 | 56 |
Sử dụng phần mềm Geogebra ta có Hình 3.1.
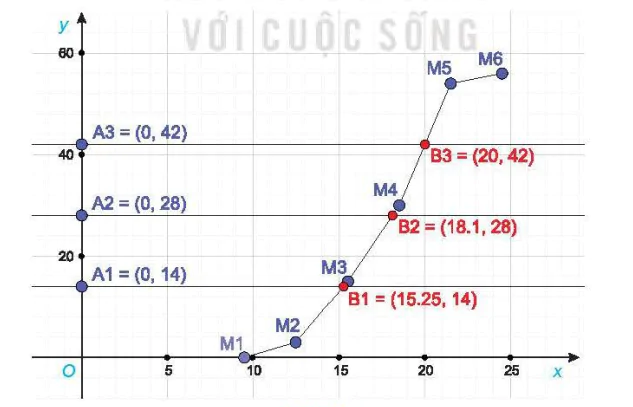
Hình 3.1
Từ hình vẽ ta có 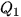 = 15,25;
= 15,25; 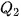 = 18,1;
= 18,1; 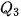 = 20.
= 20.









































































Bình Luận
Để Lại Bình Luận Của Bạn