Nội Dung Chính
Trang 104
Chương này trình bày khái niệm giới hạn của dãy số, của hàm số và một số định lí, quy tắc tìm giới hạn. Chúng là cơ sở cho việc nghiên cứu các nội dung khác của Giải tích và cho phép giải quyết nhiều bài toán của khoa học và thực tiễn. Khái niệm hàm số liên tục và một vài tính chất đơn giản của chúng được trình bày ở phần cuối chương.
| THUẬT NGỮ • Giới hạn của dãy số • Các phép toán giới hạn • Cấp số nhân lùi vô hạn • Tổng của cấp số nhân lùi vô hạn | KIẾN THỨC, KĨ NĂNG • Nhận biết khái niệm giới hạn của dãy số. • Giải thích một số giới hạn cơ bản. • Vận dụng các phép toán giới hạn đề tìm giới hạn của một số dãy số đơn giản. • Tính tổng của một cấp số nhân lùi vô hạn và vận dụng được kết quả đó để giải quyết một số tình huống thực tiễn giả định hoặc liên quan đến thực tiễn. |
Nghịch lí Zeno. Achilles (A-sin, một nhân vật trong thần thoại Hy Lạp, được mô tả là có thể chạy nhanh như gió) đuổi theo một con rùa trên một đường thẳng. Vị trí xuất phát của Achilles là 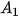

Hình 5.1
Thật vậy, trước tiên Achilles phải đến được vị trí 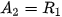 và trong khoảng thời gian này, rùa đã di chuyển đến vị trí
và trong khoảng thời gian này, rùa đã di chuyển đến vị trí 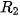 . Sau đó, Achilles phải đến được vị trí
. Sau đó, Achilles phải đến được vị trí 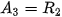 , lúc này rùa đã di chuyển đến vị trí
, lúc này rùa đã di chuyển đến vị trí 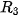
Zeno (490 – 429 trước Công nguyên) là một triết gia Hy Lạp, đến từ thành phố Elea (miền nam nước Ý ngày nay). Trong số các nghịch lí của Zeno, nghịch lí Achilles đuổi rùa được coi là đã thúc đẩy sự hình thành khái niệm giới hạn, một công cụ thiết yếu của toán học, được sử dụng để nghiên cứu các quá trình liên quan đến sự vô hạn.
Trang 105
1. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ
HĐ1. Nhận biết dãy số có giới hạn là 0
Cho dãy số (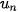 ) với
) với 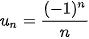 .
.
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ 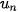 đến 0 nhỏ hơn 0,01
đến 0 nhỏ hơn 0,01
Ta nói dãy số (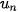 ) có giới hạn là 0 khi n dần tới dương vô cực, nếu | ) có giới hạn là 0 khi n dần tới dương vô cực, nếu |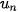 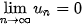 hay hay 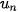 → 0 khi n → +∞. → 0 khi n → +∞. |
Ví dụ 1. Xét dãy số 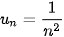 . Giải thích vì sao dãy số này có giới hạn là 0.
. Giải thích vì sao dãy số này có giới hạn là 0.
Giải
Dãy số này có giới hạn là 0, bởi vì 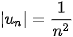 có thể nhỏ hơn một số dương bé tuỳ ý khi n đủ lớn. Chẳng hạn, để |
có thể nhỏ hơn một số dương bé tuỳ ý khi n đủ lớn. Chẳng hạn, để |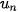
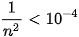 , ta cần
, ta cần 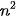 >10 000 hay n >100. Như vậy, các số hạng của dãy kể từ số hạng thứ 101 đều có giá trị tuyệt đối nhỏ hơn 0,0001.
>10 000 hay n >100. Như vậy, các số hạng của dãy kể từ số hạng thứ 101 đều có giá trị tuyệt đối nhỏ hơn 0,0001. Chú ý. Từ định nghĩa dãy số có giới hạn 0, ta có các kết quả sau:
• 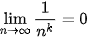 với k là một số nguyên dương;
với k là một số nguyên dương;
• 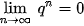 nếu |q| < 1;
nếu |q| < 1;
• Nếu |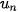
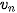 với mọi n ≥ 1 và lim
với mọi n ≥ 1 và lim 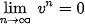 thì
thì 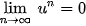 .
. Luyện tập 1. Chứng minh rằng 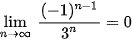 .
.
HĐ2. Nhận biết dãy số có giới hạn hữu hạn
Cho dãy số (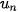
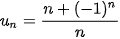 . Xét dãy số (
. Xét dãy số (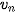 ) xác định bởi
) xác định bởi 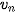 =
= 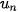 −1.
−1. Tính 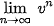
Ta nói dãy số (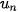 ) có giới hạn là số thực a khi n dần tới dương vô cực nếu ) có giới hạn là số thực a khi n dần tới dương vô cực nếu 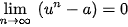 , kí hiệu , kí hiệu 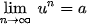 hay hay 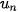 → a khi n→ +∞. → a khi n→ +∞. |
Trang 106
Ví dụ 2. Xét dãy số (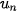
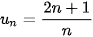 . Chứng minh rằng
. Chứng minh rằng 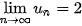 .
. Giải
Ta có 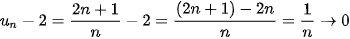 khi n → +∞.
khi n → +∞.
Do vậy 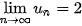 .
.
Chú ý. Nếu 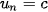
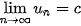 .
. 
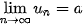 khi và chỉ khi
khi và chỉ khi 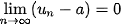 .
.
Luyện tập 2. Cho dãy số (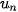
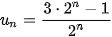 . Chứng minh rằng
. Chứng minh rằng 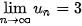 .
. Vận dụng 1. Một quả bóng cao su được thả từ độ cao 5 m xuống một mặt sàn. Sau mỗi lần chạm sàn, quả bóng nảy lên độ cao bằng 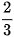 độ cao trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Giả sử
độ cao trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Giả sử 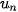 là độ cao (tính bằng mét) của quả bóng sau lần nảy lên thứ 1. Chứng minh rằng dãy số (
là độ cao (tính bằng mét) của quả bóng sau lần nảy lên thứ 1. Chứng minh rằng dãy số (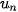
2. ĐỊNH LÍ VỀ GIỚI HẠN HỮU HẠN CỦA DÃY SỐ
HĐ3. Hình thành quy tắc tính giới hạn
Cho hai dãy số (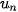 ) và (
) và (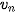 ) với
) với 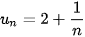 ,
, 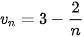 .
.
Tính và so sánh: 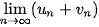
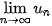 +
+ 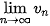 .
. Tổng quát, ta có các quy tắc tính giới hạn sau đây:
a) Nếu 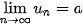 và lim và lim 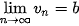 thì thì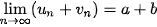 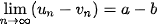 ; ;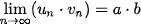 ; ;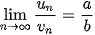 nếu b # 0. nếu b # 0.b) Nếu 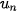 ≥ 20 với mọi n và ≥ 20 với mọi n và 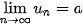  . . |
Ví dụ 3. Tìm  .
.
Giải
Áp dụng các quy tắc tính giới hạn, ta được
 .
.
Để tính giới hạn của dãy số dạng phân thức, ta chia cả tử thức và mẫu thức cho luỹ thừa cao nhất của n, rồi áp dụng các quy tắc tính giới hạn.

Trang 107
Luyện tập 3. Tìm 
3. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN
HĐ4. Làm quen với việc tính tổng vô hạn
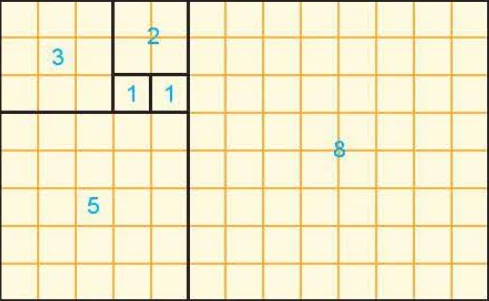
Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình vuông nhỏ bằng nhau, sau đó tô màu hình vuông nhỏ góc dưới bên trái (H.5.2). Lặp lại các thao tác này với hình vuông nhỏ góc trên bên phải. Giả sử quá trình trên tiếp diễn vô hạn lần. Gọi 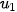 ,
, 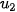 ,...,
,..., 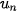 ,.... lần lượt là độ dài cạnh của các hình vuông được tô màu.
,.... lần lượt là độ dài cạnh của các hình vuông được tô màu.
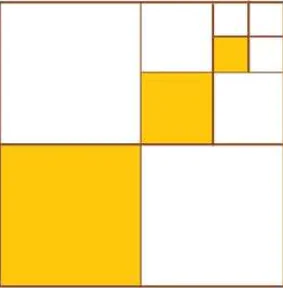
Hình 5.2
a) Tính tổng 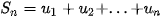
b) Tìm 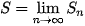 .
.
Cấp số nhân vô hạn (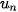 ) có công bội q với |q| < 1 được gọi là cấp số nhân lùi vô hạn. Cho cấp số nhân lùi vô hạn (
) có công bội q với |q| < 1 được gọi là cấp số nhân lùi vô hạn. Cho cấp số nhân lùi vô hạn (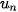 ) với công bội q. Khi đó
) với công bội q. Khi đó
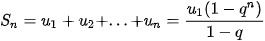 .
.
Vì |q| < 1 nên 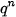
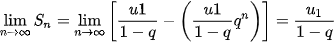 .
.
Giới hạn này được gọi là tổng của cấp số nhân lùi vô hạn (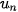 ), và kí hiệu là
), và kí hiệu là 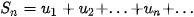
Như vậy
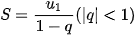 . . |
Ví dụ 4. Tính tổng 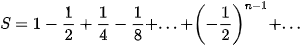
Giải
Đây là tổng của cấp số nhân lùi vô hạn với 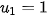 và
và 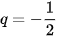 .
.
Do đó 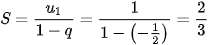 .
.
Trang 108
Ví dụ 5. Biểu diễn số thập phân vô hạn tuần hoàn 2,222.... dưới dạng phân số.
Giải
Ta có 2,222... = 2 + 0,2 + 0,02 + 0,002 + ... = 2 + 2 
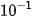

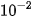 + 2
+ 2 
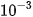 + ...
+ ... Đây là tổng của cấp số nhân lùi vô hạn với 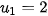
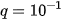 nên
nên 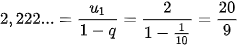 .
.
Luyện tập 4. Tính tổng 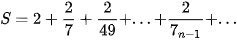
Vận dụng 2. (Giải thích nghịch lí Zeno)
Để đơn giản, ta giả sử Achilles chạy với vận tốc 100 km/h, vận tốc của rùa là 1 km/h và khoảng cách ban đầu a = 100 (km).
a) Tính thời gian 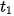 ,
, 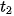
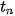 ,.... tương ứng để Achilles đi từ
,.... tương ứng để Achilles đi từ 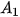 đến
đến 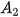 , từ
, từ 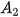 đến
đến 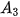
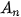 đến
đến 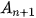 ,...
,... b) Tinh tổng thời gian cần thiết để Achilles chạy hết các quãng đường A,A,, A.A... A, Ana ..., tức là thời gian cần thiết để Achilles đuổi kịp rùa.
c) Sai lầm trong lập luận của Zeno là ở đâu?
4. GIỚI HẠN VÔ CỰC CỦA DÃY SỐ
HĐ5. Nhận biết giới hạn vô cực
Một loại vi khuẩn được nuôi cấy với số lượng ban đầu là 50. Sau mỗi chu kì 4 giờ, số lượng của chúng sẽ tăng gấp đôi.
a) Dự đoán công thức tính số vi khuẩn 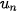 sau chu kì thứ n.
sau chu kì thứ n.
b) Sau bao lâu, số lượng vi khuẩn sẽ vượt con số 10 000?
• Dãy số (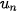 ) được gọi là có giới hạn +∞ khi n → +∞ nếu ) được gọi là có giới hạn +∞ khi n → +∞ nếu 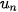 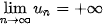 hay hay  → +∞ khi n → +∞. → +∞ khi n → +∞.• Dãy số ( 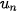 ) được gọi là có giới hạn -∞ khi n → +∞ nếu ) được gọi là có giới hạn -∞ khi n → +∞ nếu 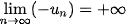 , kí hiệu , kí hiệu 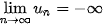 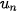 → -∞ khi n → +∞. → -∞ khi n → +∞. |
Theo định nghĩa trên, ta có:
• 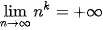 , với k là số nguyên dương;
, với k là số nguyên dương;
• 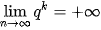 với q>1.
với q>1.
Trang 109
Liên quan đến giới hạn vô cực của dãy số, ta có một số quy tắc sau đây.
• Nếu 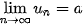 và và 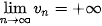 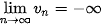 ) thì ) thì 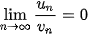 . .• Nếu 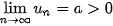 , , 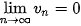 và và 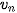 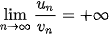 . .• Nếu 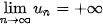 và và 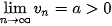 thì thì 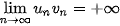 . . |
Ví dụ 6. Tính 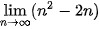
Giải
Ta có 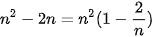 . Hơn nữa
. Hơn nữa 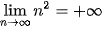 và
và 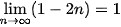 .
.
Do đó 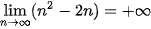 .
.
Luyện tập 5. Tính 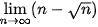
BÀI TẬP
5.1. Tìm các giới hạn sau:
a) 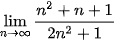 ;
;
b) 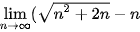
5.2. Cho hai dãy số không âm (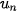 ) và (v_n) với
) và (v_n) với 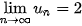 và
và 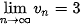
a) 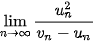 ;
;
b) 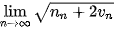 .
.
5.3. Tìm giới hạn của các dãy số cho bởi:
a) 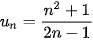
b) 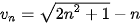 .
.
5.4. Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số:
a) 1,(12) = 1,121212...;
b) 3,(102) = 3,102102102...
5.5. Một bệnh nhân hàng ngày phải uống một viên thuốc 150 mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
5.6. Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ 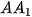
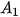 kẻ
kẻ 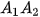 ⊥ AC, sau đó lại kẻ
⊥ AC, sau đó lại kẻ 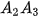 ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn A
⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn A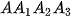 ... Tính độ dài đường gấp khúc này theo h và α.
... Tính độ dài đường gấp khúc này theo h và α. 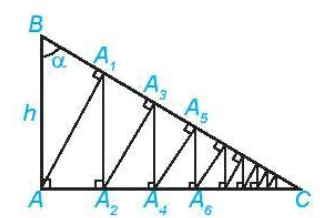
Hình 53
Trang 110
Em có biết?
Dãy số Fibonacci và tỉ lệ vàng
Ta đã biết dãy Fibonacci cho bởi hệ thức truy hồi:
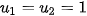 ,
, 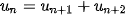 với n >2.
với n >2.
Chia hai vế cho 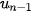 và đặt
và đặt 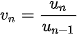 , ta có công thức
, ta có công thức 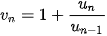
Dãy (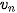 ) có giới hạn là một số dương r thoả mãn phương trình r = 1+
) có giới hạn là một số dương r thoả mãn phương trình r = 1+ 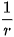 hay tương đương
hay tương đương 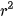 − r − 1 = 0. Giải phương trình này ta được
− r − 1 = 0. Giải phương trình này ta được 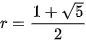
Đây chính là tỉ lệ vàng (golden ratio) được sử dụng trong kiến trúc, hội hoạ, tôn giáo, ... Dãy Fibonacci và tỉ lệ vàng cũng xuất hiện nhiều trong thế giới tự nhiên.
Dãy số logistic
Trong sinh thái học, người ta sử dụng dãy (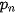 )cho bởi công thức truy hồi
)cho bởi công thức truy hồi 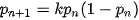 để mô phỏng hệ sinh thái của một loài (động vật hoặc thực vật), trong đó
để mô phỏng hệ sinh thái của một loài (động vật hoặc thực vật), trong đó  là tỉ lệ giữa số lượng cá thể theo thời gian và sức chứa của môi trường, k là hệ số phụ thuộc đặc điểm của loài và điều kiện môi trường. Dãy số này được gọi là dãy logistic, do nhà sinh học Robert May đưa ra năm 1976. Tuỳ thuộc hệ số k và giá trị ban đầu P. ta có thể dự đoán sự thay đổi của hệ trong tương lai. Đặc biệt, trong trường hợp dãy (
là tỉ lệ giữa số lượng cá thể theo thời gian và sức chứa của môi trường, k là hệ số phụ thuộc đặc điểm của loài và điều kiện môi trường. Dãy số này được gọi là dãy logistic, do nhà sinh học Robert May đưa ra năm 1976. Tuỳ thuộc hệ số k và giá trị ban đầu P. ta có thể dự đoán sự thay đổi của hệ trong tương lai. Đặc biệt, trong trường hợp dãy ( ) có giới hạn là một số dương, ta nói hệ sinh thái của loài là ổn định.
) có giới hạn là một số dương, ta nói hệ sinh thái của loài là ổn định.
(Theo Stewart, Calculus, Nhà xuất bản Cengage Learning)










































































Bình Luận
Để Lại Bình Luận Của Bạn