Nội Dung Chính
Trang 92
MỤC TIÊU
Sử dụng phần mềm GeoGebra, vẽ vectơ tổng của ba vectơ cho trước.
Hoạt động: Lấy bốn điểm A, B, C, D trong không gian ba chiều và vẽ vectơ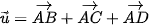 
Hướng dẫn thực hiện:
Bước 1. Mở phần mềm GeoGebra, vào mục Phối cảnh \ Vẽ đồ hoạ 3D (H.T.4).
Bấm chuột trái, chọn "Hiển thị hệ trục toạ độ" để tắt phần hiển thị hệ trục toạ độ (H.T.5).
GeoGebra Classic
Graphing
Hình học
Vẽ đồ họa 3D
complex adaptive system
Trang trống trong Excel
Xác suất
Tải tập tin
Hình T.4
Hiện thị hệ trục tọa độ
Show Plane
Hiển thị lưới Thanh điều hướng
Phóng to / thu nhỏ
Hiển thị tất cả các đối tượng
Góc nhìn mặc định
Hiển thị dạng 3D ...
Hình T.5
Bước 2. Chọn công cụ "Điểm mới” để vẽ các điểm A, B, C, D trên mặt phẳng màu xám (H.T.6).
Điểm mới
Điểm thuộc đối tượng
Giao điểm của 2 đối tượng
Trung điểm hoặc tâm
Dán / hủy dán điểm
Hình T.6
Chú ý. Ta có thể di chuyển các điểm bằng cách kích chuột phải vào điểm để hiện ra các mũi tên di chuyển 4 chiều và 2 chiều, sau đó di chuyển điểm theo hướng tương ứng với
chiều mũi tên.
Bước 3. Sử dụng công cụ vẽ vectơ qua 2 điểm (H.T.7) để vẽ ba vecto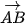 
, 
. 
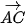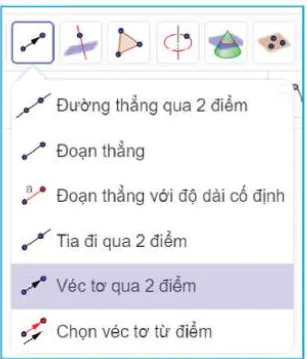
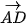Đường thẳng qua 2 điểm
Đoạn thẳng
Đoạn thẳng với độ dài cố định
Tia đi qua 2 điểm
Véc tơ qua 2 điểm
Chọn véc tơ từ điểm
Hình 1.7
Bước 4. Sử dụng công cụ “Đường song song” (H.T.8) để vẽ các đường thẳng song song với các vectơ ,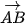
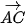
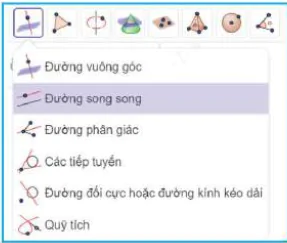
Đường vuông góc
Đường song song
Đường phân giác
Các tiếp tuyến
Đường đối cực hoặc đường kính kéo dài
Qũy tích
Hình T.8
Trang 93
Xác định giao điểm E của hai đường thẳng đó bằng công cụ "Giao điểm của 2 đối tượng”. Vẽ vectơ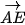 
.
Theo nguyên tắc hình bình hành, ta có: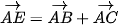 
.
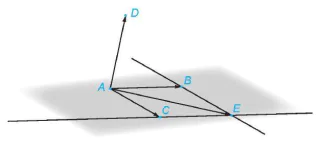
Hình T.9
Bước 5. Sử dụng công cụ vẽ đường thẳng song song để vẽ các đường thẳng song song với các vectơ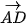
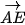và xác định giao điểm F của hai đường thẳng đó.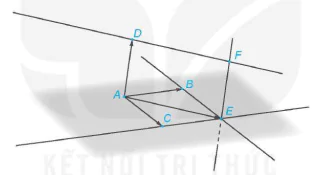 
Hình 1.10
Bước 6. Về vectơ .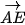
Theo nguyên tắc hình bình hành, ta có: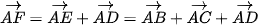 
.
Vậy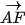 
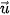cần dựng.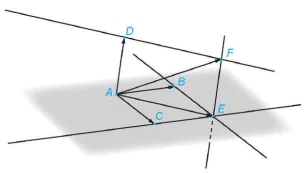 
Hình T.11
Các Bài Học Khác
Kết nối tri thức NXB Giáo Dục Việt Nam Toán 12 tập 1 Hoạt Động Thực Hành Trải Nghiệm Độ Dài Gang Tay (Gang Tay Của Bạn Dài Bao Nhiêu?)
Xem thêm ⟶
Kết nối tri thức NXB Giáo Dục Việt Nam Toán 12 tập 1 Hoạt Động Thực Hành Trải Nghiệm Bảng tra cứu từ ngữ
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn