Nội Dung Chính
Trang 67
| KIẾN THỨC, KĨ NĂNG • Nhận biết biểu thức toạ độ của các phép toán vectơ trong không gian, thể hiện các phép toán vectơ theo toạ độ, xác định độ dài của một vectơ khi biết toạ độ hai đầu mút. • Vận dụng biểu thức toạ độ của các phép toán vectơ để giải một số bài toán có liên quan đến thực tiễn. |
Những căn nhà gỗ trong Hình 2.47a được phác thảo dưới dạng một hình lăng trụ đứng tam giác OAB.O'A'B' như trong Hình 2.47b. Với hệ trục toạ độ Oxyz thể hiện như Hình 2.47b (đơn vị đo lấy theo centimét), hai điểm A' và B' có toạ độ lần lượt là (240; 450; 0) và (120; 450; 300). Từ những thông tin trên, có thể tính được kích thước mỗi chiều của những căn nhà gỗ hay không?

Hình 2.47
1. BIỂU THỨC TOẠ ĐỘ CỦA PHÉP CỘNG HAI VECTƠ, PHÉP TRỪ HAI VECTƠ, PHÉP NHÂN MỘT SỐ VỚI MỘT VECTƠ
HĐ1. Hình thành biểu thức toạ độ của phép cộng hai vectơ, phép trừ hai vectơ, phép nhân một số với một vectơ trong không gian
Trong không gian Oxyz, cho hai vectơ 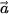 = (1; 0; 5) và
= (1; 0; 5) và 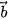 = (1; 3; 9).
= (1; 3; 9).
a) Biểu diễn hai vectơ 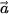 và
và 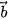 qua các vectơ đơn vị
qua các vectơ đơn vị 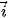
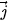 ,
, 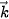 .
. b) Biểu diễn hai vectơ 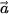 +
+ 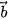 và 2
và 2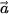
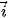 ,
, 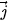 ,
, 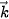 , từ đó xác định toạ độ của hai vectơ đó.
, từ đó xác định toạ độ của hai vectơ đó. Trong không gian Oxyz, cho hai vectơ 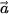 = (x, y, z) và = (x, y, z) và 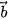 • 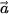 + b=(x + x'; y + y'; z + z'); + b=(x + x'; y + y'; z + z');• 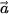 - b = (x - x'; y - y'; z - z'); - b = (x - x'; y - y'; z - z');• k 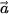 = (kx, ky; kz) với k là một số thực. = (kx, ky; kz) với k là một số thực. |
 Nếu toạ độ của vectơ
Nếu toạ độ của vectơ 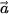
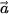 là gì?
là gì? Trang 68
Nhận xét. Vectơ 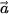 =(x; y; z) cùng phương với vectơ
=(x; y; z) cùng phương với vectơ 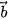 = (x'; y'; z') ≠
= (x'; y'; z') ≠ 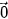 khi và chỉ khi tồn tại số thực k sao cho
khi và chỉ khi tồn tại số thực k sao cho 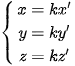
Ví dụ 1. Trong không gian Oxyz, cho hai vectơ 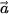 = (2; 1; 5) và
= (2; 1; 5) và 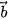 = (2; 2; 1). Tìm toạ độ của mỗi vectơ sau:
= (2; 2; 1). Tìm toạ độ của mỗi vectơ sau:
a) 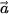 -
- 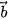 ;
;
b) 3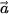
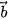 .
. Giải
a) Vì 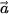 =(2; 1; 5) và
=(2; 1; 5) và 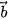 = (2; 2; 1) nên
= (2; 2; 1) nên 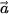 –
– 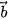
b) Ta có 3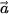 = (3 · 2; 3 · 1; 3 · 5) = (6; 3; 15) và 2
= (3 · 2; 3 · 1; 3 · 5) = (6; 3; 15) và 2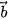 = (2 · 2; 2 · 2; 2 · 1) = (4; 4; 2).
= (2 · 2; 2 · 2; 2 · 1) = (4; 4; 2).
Do đó 3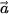 + 2
+ 2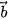 = (6 + 4; 3 + 4; 15 + 2) = (10; 7; 17).
= (6 + 4; 3 + 4; 15 + 2) = (10; 7; 17).
Luyện tập 1. Trong không gian Oxyz, cho ba vectơ 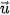
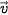 =(-1; 3; –2) và
=(-1; 3; –2) và 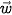 = (0; 5; 4). Tìm toạ độ của vecto
= (0; 5; 4). Tìm toạ độ của vecto 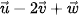 .
. HĐ2. Thiết lập toạ độ trung điểm đoạn thẳng, toạ độ trọng tâm tam giác
Trong không gian Oxyz, cho tam giác ABC có A(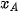 ;
; 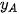
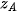 ), B(
), B(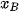 ;
; 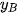 ;
; 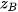 ) và C(
) và C(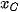
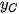 ;
; 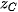 ).
). a) Gọi M là trung điểm của đoạn thẳng AB. Tìm toạ độ của M theo toạ độ của A và B.
b) Gọi G là trọng tâm của tam giác ABC. Tìm toạ độ của G theo toạ độ của A, B và C.
Ta đã biết: ;
; .
.
Trong không gian Oxyz, cho ba điểm không thẳng hàng A(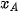 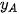 ; ; 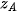 ), B( ), B(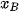 ; ; 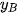 ; ; 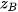 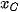 ; ; 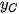 ; ; 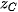 ). Khi đó: ). Khi đó:- Toạ độ trung điểm của đoạn thẳng AB là 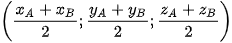 ; ;- Toạ độ trọng tâm của tam giác ABC là  |
Ví dụ 2. Trong không gian Oxyz, cho ba điểm A(1; 2; 3), B(3; 2; 1) và C(2; –1; 5). Tìm toạ độ trung điểm M của đoạn thẳng AB và toạ độ trọng tâm G của tam giác ABC.
Giải
Vì M là trung điểm của đoạn thẳng AB nên toạ độ của điểm M là 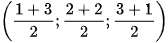 suy ra M(2; 2; 2).
suy ra M(2; 2; 2).
Vì G là trọng tâm của tam giác ABC nên toạ độ của điểm G là  suy ra G(2; 1; 3).
suy ra G(2; 1; 3).
Trang 69
Luyện tập 2. Trong không gian Oxyz, cho ba điểm A(2; 9; −1), B(9; 4; 5) và G(3; 0; 4). Tìm toạ độ điểm C sao cho tam giác ABC nhận G là trọng tâm.
2. BIỂU THỨC TOẠ ĐỘ CỦA TÍCH VÔ HƯỚNG
HĐ3. Thiết lập biểu thức toạ độ của tích vô hướng trong không gian
Trong không gian Oxyz, cho hai vectơ 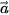 = (x; y; z) và
= (x; y; z) và 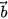 = (x'; y'; z').
= (x'; y'; z').
a) Giải thích vì sao 
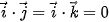 .
. b) Sử dụng biểu diễn  để tính các tích vô hướng
để tính các tích vô hướng  ,
, 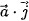 và
và 
c) Sử dụng biểu diễn  để tính tích vô hướng
để tính tích vô hướng  .
.
Trong không gian Oxyz, tích vô hướng của hai vectơ 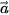 = (x; y; z) và = (x; y; z) và 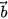 = (x'; y'; z') được xác định bởi công thức: = (x'; y'; z') được xác định bởi công thức: |
Nhận xét
– Hai vectơ 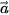 và
và 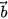 vuông góc với nhau nếu và chỉ nếu xx' + yy' + zz' = 0.
vuông góc với nhau nếu và chỉ nếu xx' + yy' + zz' = 0.
– Nếu 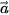 = (x, y; z) thì
= (x, y; z) thì  .
.
– Nếu 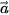
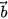 = (x'; y'; z') là hai vectơ khác
= (x'; y'; z') là hai vectơ khác 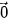 thì
thì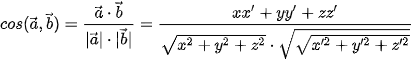 .
. Ví dụ 3. Trong không gian Oxyz, cho hai vectơ 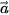 = (1; 4; 2) và
= (1; 4; 2) và 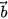
a) Tính  và cho biết hai vectơ
và cho biết hai vectơ 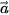 và
và 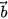 có vuông góc với nhau hay không.
có vuông góc với nhau hay không.
b) Tính độ dài của vectơ 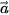 .
.
Giải
a) Ta có: 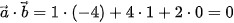
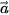 và
và 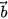 vuông góc với nhau.
vuông góc với nhau. b) Độ dài của vectơ 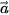 là
là  .
.
Luyện tập 3. Trong Ví dụ 3, tính 
Ví dụ 4. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA vuông góc với mặt phẳng (ABCD). Giả sử SA = 2, AB = 3, AD = 4. Xét hệ toạ độ Oxyz với O trùng A và các tia Ox, Oy, Oz lần lượt trùng với các tia AB, AD, AS (H.2.48).
a) Xác định toạ độ của các điểm S, A, B, C, D.
b) Tính BD và SC.
c) Tính 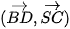 .
.

Hình 2.48
Giải
a) Vì A trùng gốc toạ độ nên A(0; 0; 0). Vì B thuộc tia Ox và AB = 3 nên B(3; 0; 0). Vì D thuộc tia Oy và AD = 4 nên D(0; 4; 0). Vì S thuộc tia Oz và AS = 2 nên S(0; 0; 2). Vì hình chiếu của C lên các trục Ox, Oy, Oz lần lượt là B, D, A nên C(3; 4; 0).
Trang 70
b) Ta có 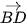 = (0 - 3, 4 - 0; 0 - 0) = (–3; 4; 0), suy ra
= (0 - 3, 4 - 0; 0 - 0) = (–3; 4; 0), suy ra 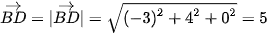 .
.
Ta có 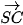
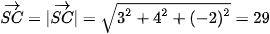 .
. c) Ta có 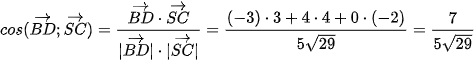 , suy ra
, suy ra 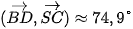 .
.
Chú ý. Nếu A(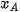 ;
; 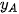
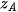 ) và B(
) và B(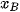 ;
; 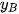 ;
; 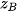 ) thì
) thì 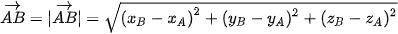
Đặc biệt, khi B trùng O ta nhận được công thức  .
.
Luyện tập 4. Trong không gian Oxyz, cho A(0; 2; 1), B(3; 2; 1) và C(-2; 5; 7).
a) Tính chu vi của tam giác ABC.
b) Tính 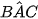 .
.
3. VẬN DỤNG TOẠ ĐỘ CỦA VECTƠ TRONG MỘT SỐ BÀI TOÁN CÓ LIÊN QUAN ĐẾN THỰC TIỄN
Ví dụ 5. Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo kilômét), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800; 500; 7) đến điểm B(940; 550; 8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo là gì?

Hình 2.49
Giải (H.2.49)
Gọi C(x; y, z) là vị trí của máy bay sau 5 phút tiếp theo. Vì hướng của máy bay không đổi nên 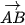 và
và 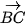
Do đó  .
.
Mặt khác,  nên
nên  .
.
Từ đó  và vì vậy C(1 010; 575; 8,5).
và vì vậy C(1 010; 575; 8,5).
Vậy toạ độ của máy bay sau 5 phút tiếp theo là (1 010; 575; 8,5).
Trang 71
Luyện tập 5. Với các giả thiết như trong Ví dụ 5, hãy xác định toạ độ của chiếc máy bay sau 10 phút tiếp theo (tính từ thời điểm máy bay ở điểm B).
Ví dụ 6. Hãy trả lời câu hỏi trong tình huống mở đầu.
Giải. Vì điểm A' có toạ độ là (240; 450; 0) nên khoảng cách từ A' đến các trục Ox, Oy lần lượt là 450 cm và 240 cm. Suy ra A'A = 450 cm và A'O' = 240 cm. Từ giả thiết suy ra 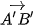
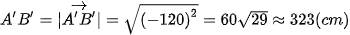 .
. Vì O'O = A'A = 450 cm và O' nằm trên trục Oy nên toạ độ của điểm O' là (0; 450; 0).
Do đó 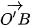 = (120; 0; 300) và
= (120; 0; 300) và 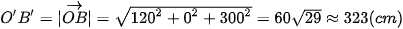 .
.
Vậy mỗi căn nhà gỗ có chiều dài là 450 cm, chiều rộng là 240 cm, mỗi cạnh bên của mặt tiền có độ dài là 323 cm.
Luyện tập 6. Trong tình huống mở đầu, hãy tính độ lớn của góc α.
| Góc α chính là góc giữa mặt bên của căn nhà gỗ và mặt đất |
Ví dụ 7. Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất nằm cách điểm xuất phát 2 km về phía nam và 1 km về phía đông, đồng thời cách mặt đất 0,5 km. Chiếc thứ hai nằm cách điểm xuất phát 1 km về phía bắc và 1,5 km về phía tây, đồng thời cách mặt dát 0,8 km.
Chọn hệ trục toạ độ Oxyz với gốc O đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng (Oxy) trùng với mặt đất với trục Ox hướng về phía nam, trục Oy hướng về phía đông và trục Oz hướng thẳng đứng lên trời (H.2.50), đơn vị đo lấy theo kilômét.
a) Tìm toạ độ của mỗi chiếc khinh khí cầu đối với hệ toạ độ đã chọn.
b) Xác định khoảng cách giữa hai khinh khí cầu (làm tròn kết quả đến chữ số thập phân thứ hai).

Hình 2.50
Giải
a) Chiếc khinh khí cầu thứ nhất và thứ hai có toạ độ lần lượt là (2; 1; 0,5) và (–1; –1,5; 0,8).
b) Khoảng cách giữa hai chiếc khinh khí cầu là

Trang 72
Luyện tập 7. Trong Ví dụ 7, khinh khí cầu thứ nhất hay thứ hai ở xa điểm xuất phát hơn? Giải thích vì sao.
BÀI TẬP
2.20. Trong không gian Oxyz, cho ba vectơ 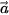 =(3; 1; 2),
=(3; 1; 2), 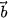 =(−3; 0; 4) và
=(−3; 0; 4) và 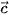 = (6; –1; 0).
= (6; –1; 0).
a) Tìm toạ độ của các vectơ 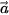 +
+ 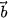
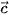 và 2
và 2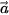 – 3
– 3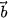 – 5
– 5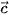 .
. b) Tính các tích vô hướng 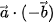
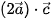 .
. 2.21. Trong không gian Oxyz, cho ba điểm M(–4; 3; 3), N(4; –4; 2) và P(3; 6; −1).
a) Tìm toạ độ của các vectơ 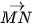 ,
, 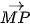 , từ đó chứng minh rằng ba điểm M, N, P không thẳng hàng.
, từ đó chứng minh rằng ba điểm M, N, P không thẳng hàng.
b) Tìm toạ độ của vectơ  , từ đó suy ra toạ độ của điểm Q sao cho tứ giác MNPQ là hình bình hành.
, từ đó suy ra toạ độ của điểm Q sao cho tứ giác MNPQ là hình bình hành.
c) Tính chu vi của hình bình hành MNPQ.
2.22. Trong không gian Oxyz, cho tam giác ABC có A(1; 0; 1), B(0; –3; 1) và C(4; −1; 4).
a) Tìm toạ độ trọng tâm của tam giác ABC.
b) Chứng minh rằng 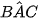
c) Tính  .
.
2.23. Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8 m, chiều rộng là 6 m và chiều cao là 3 m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục toạ độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét (H.2.51). Hãy tìm toạ độ của điểm treo đèn.

Hình 2.51
2.24. Trong không gian, xét hệ toạ độ Oxyz có gốc O trùng với vị trí của một giàn khoan trên biển, mặt phẳng (Oxy) trùng với mặt biển (được coi là phẳng) với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời (H.2.52). Đơn vị đo trong không gian Oxyz lấy theo kilômét. Một chiếc ra đa đặt tại giàn khoan có phạm vi theo dõi là 30 km. Hỏi ra đa có thể phát hiện được một chiếc tàu thám hiểm có toạ độ là (25; 15; –10) đối với hệ toạ độ nói trên hay không? Hãy giải thích vì sao.

Hình 2.52



































































Bình Luận
Để Lại Bình Luận Của Bạn