Nội Dung Chính
Trang 99
BẢNG TRA CỨU TỪ NGỮ
B Bảng biến thiên 7
Bài toán tối ưu hoá 35
C Cao độ 61
Cực đại 9
Cực tiểu 9
Cực trị 9
Chi phí biên 34
D-Đ Điểm cực đại của đồ thị 9
Điểm cực tiểu của đồ thị 9
Điểm cực trị 9
Độ lệch chuẩn 80
Đồ thị hàm số 6
Đồng biến 6
Đơn điệu 7
Độ dài của vectơ 46
G Giá trị cực đại 9
Giá trị cực tiểu 9
Giá trị lớn nhất 15
Giá trị nhỏ nhất 15
Gia tốc tức thời 33
Góc giữa hai vectơ 55
H Hai vectơ bằng nhau 47
Hai vectơ cùng phương 47
Hàm cầu 38
Hàm chi phí 34
Hàm doanh thu 38
Hàm doanh thu biên 38
Hàm lợi nhuận 38
Khoảng biến thiên 76
Khoảng tứ phân vị 77
Hàm lợi nhuận biên 38
Hệ toạ độ Oxyz 60
Hoành độ 61
K Khảo sát sự biến thiên của hàm số 26
L-P Mặt phẳng toạ độ 60
Nghịch biến 6
Phương sai 80
Quy tắc xét tính đơn điệu 8
Quy tắc tìm cực trị 11
T Tâm đối xứng của đô thị 27
Tập xác định của hàm số 8
Tích vô hướng của hai vectơ 56
Tiệm cận đứng 21
Tiệm cận ngang 20
Tiệm cận xiên 23
Toạ độ của điểm 61
Toạ độ của vecto 63
Tốc độ thay đổi tức thời 33
Tốc độ tăng trưởng tức thời 33
Tốc độ phản ứng tức thời 33
Tung độ 61
Tứ phân vị thứ nhất 77
Tứ phân vị thứ ba 77
Vận tốc tức thời 33
Vectơ đơn vị 60
Trang 100
BẢNG GIẢI THÍCH THUẬT NGỮ
| Thuật ngữ | Giải thích |
| Cực trị của hàm số | Giá trị cực đại hoặc giá trị cực tiểu của hàm số |
| Điểm cực trị của đồ thị hàm số | Điểm (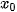 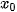 )), trong đó x, là điểm cực trị của hàm số f(x) )), trong đó x, là điểm cực trị của hàm số f(x) |
| Điểm cực trị của hàm số | Điểm cực trị của hàm số là giá trị của biến số mà tại đó hàm số đạt cực trị |
| Giá trị lớn nhất của hàm số | Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) ≤ M với mọi x ∈ D và tồn tại 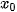 ∈ D sao cho f( ∈ D sao cho f(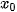 ) = M ) = M |
| Giá trị nhỏ nhất của hàm số | Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) ≥ m với mọi x ∈ D và tồn tại 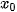 ∈ D sao cho f( ∈ D sao cho f(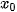 |
| Góc giữa hai vectơ trong không gian | Góc AOB, trong đó 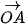 và và 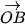 là hai vectơ chung gốc và lần lượt bằng hai vectơ khác là hai vectơ chung gốc và lần lượt bằng hai vectơ khác 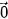 đã cho đã cho |
| Hệ toạ độ trong không gian | Hệ gồm ba trục vuông góc với nhau từng đối một với ba vectơ đơn vị trên ba trục |
| Khảo sát hàm số | Việc tìm tập xác định, xét chiều biến thiên, tìm cực trị, tìm các giới hạn đặc biệt của hàm số đó và thể hiện các kết quả này trong bảng biến thiên |
| Khoảng biến thiên của mẫu số liệu ghép nhóm | Hiệu số giữa giá trị lớn nhất có thể và giá trị nhỏ nhất có thể của các giá trị trong mẫu số liệu |
| Quy tắc hình hộp | Tổng của ba vectơ là ba cạnh cùng xuất phát từ một đỉnh của hình hộp bằng vectơ đường chéo của hình hộp xuất phát từ đỉnh đó |
| Tiệm cận đứng | Đường thẳng x = 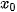 gọi là tiệm cận đứng của đồ thị hàm số y = f(x) nếu một trong các điều kiện sau được thoả mãn: gọi là tiệm cận đứng của đồ thị hàm số y = f(x) nếu một trong các điều kiện sau được thoả mãn: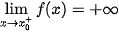 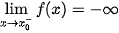 ; ; 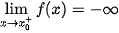 ; ; 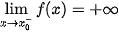 |
| Tiệm cận ngang | Đường thẳng y = 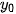 gọi là tiệm cận ngang của đồ thị hàm số | y = f(x) nếu gọi là tiệm cận ngang của đồ thị hàm số | y = f(x) nếu 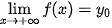 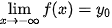 |
| Tiệm cận xiên | Đường thẳng y = ax + b (a ≠ 0) gọi là tiệm cận xiên của đồ thị hàm số y = f(x) nếu 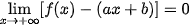 hoặc hoặc 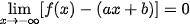 |
| Vectơ đơn vị (của trục) | Vectơ có hướng trùng với hướng của trục và có độ dài bằng 1 |




































































Bình Luận
Để Lại Bình Luận Của Bạn