Nội Dung Chính
(Trang 56)
| Sau bài này em sẽ:
|
|
Chúng ta đã biết từ bài học trước, thiết lập các thuật toán duyệt sẽ phụ thuộc hoàn toàn vào mô hình và cấu trúc của miền dữ liệu cần tìm kiếm. Từ lâu các nhà khoa học đã nhìn thấy rất nhiều bài toán khó không tìm được cách duyệt hữu hiệu, điển hình nhất là bài toán tìm đường đi trong mê cung. Bài toán tìm đường đi trong mê cung lần đầu tiên được đưa ra trong cuốn sách Récréations Mathématiques của tác giả Édouard Lucas năm 1882 tại Pháp. Cùng trong cuốn sách đó Lucas đã đưa ra phác thảo đầu tiên của một phương pháp giải bài toán tìm đường đi trong mê cung mà bây giờ chúng ta gọi là thuật toán duyệt quay lui, hay đơn giản là thuật toán quay lui (backtracking).
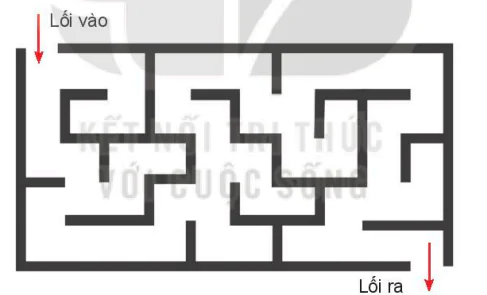
Hình 13.1. Mê cung Trong trò chơi mê cung (xem hình) em cần tìm một đường đi xuất phát từ lối vào và ra khỏi mê cung tại lối ra. Em có đề xuất gì để giải bài toán này. |
Lối vào
Lối ra
1. Kĩ thuật duyệt quay lui
| Hoạt động 1 Tìm hiểu ý tưởng của thuật toán quay lui Đọc, trao đổi và thảo luận về ý tưởng thuật toán quay lui năm 1882 của bài toán tìm đường đi trong mê cung. |
(Trang 57)
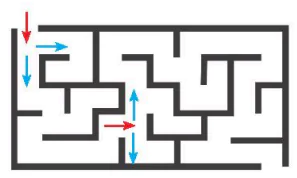
| Một đặc thù của bài toán mê cung là tại một vị trí chúng ta có thể đi tiếp theo nhiều hướng. Trong hình 13.2 chỉ ra sau mũi tên màu đỏ có thể có hai hướng đi tiếp theo (theo mũi tên màu xanh). Ý tưởng của thuật toán quay lui là thiết lập một hàm (thủ tục) xuất phát từ một vị trí hiện thời để tìm kiếm các bước đi tiếp theo. Khuôn dạng của hàm này được mô tả bằng mã giả (pseudocode) như sau: |
Hình 13.2. Cách đi trong mê cung |
1Tìm kiếm bước đi tiếp theo <//hàm>
2 Nếu vị trí hiện thời là đích
3 Thông báo tìm thấy nghiệm
4 Dừng chương trình
5 Lập trên tập hợp các khả năng có thể đi tiếp
6 Nếu bước đi là khả thi
7 Thực hiện bước đi từ vị trí hiện thời.
8 Cập nhật thông tin vào bước đi
9 Nếu không tìm được đi và quay lại trạng thái trước
10 Xoá thông tin bước đi và quay lại trạng thái trước
Giải thích: Hàm có chức năng tìm bước đi tiếp theo xuất phát từ <vị trí hiện thời>. Nếu vị trí hiện thời là đích thì thông báo tìm thấy nghiệm tại dòng 3 và dừng chương trình. Dòng 5 sẽ tìm tất cả các phương án có thể đi tiếp. Nếu tìm thấy một phương án đi khả thi tại dòng 6 thì thực hiện ngay bước đi này tại dòng 7 để cập nhật thông tin vào <vị trí> mới. Sau gọi đệ quy lại hàm gốc để đi tiếp tại dòng 9. Nếu không thể đi tiếp (lệnh gọi đệ quy dòng 9 không thể thực hiện) thì quay lui tại dòng 10, xoá thông tin bước vừa đi để quay lại vòng lặp 5.
| Ý tưởng của thuật toán duyệt quay lui là luôn tìm cách đi tiếp theo. Xử lí thật lùi lại vị trí gốc, thuật toán sẽ gọi lại hàm tìm bước đi tiếp theo. Nếu không tìm thấy đường đi thì cần “quay lui” về vị trí trước đó để tìm đường đi khác. Thuật toán sẽ sử dụng kĩ thuật đệ quy khi gọi hàm cho bước đi tiếp theo. |
1. Khi đã thực hiện hết các bước lập tại dòng 2 ở trên thì hàm có dừng không?
2. Lệnh gọi hàm chính của chương trình trên là gì?
3. Nếu yêu cầu bổ sung thêm 1 lệnh "Nếu thấy <lối ra> thì thông báo và dừng chương trình" thì lệnh này sẽ đặt ở đâu trong chương trình trên?
2. Mô tả tổng quát của thuật toán duyệt quay lui
| Hoạt động 2 Tìm hiểu mô hình tổng quát của kĩ thuật duyệt quay lui Quan sát, thực hiện và thảo luận các bước thiết kế mô hình tổng quát của kĩ thuật duyệt quay lui. |
(Trang 58)
Mô hình tổng quát của thuật toán duyệt quay lui cần được thiết kế sao cho có thể dễ dàng cài đặt trên máy tính theo ngôn ngữ lập trình bậc cao bất kì, ví dụ như Python.
Chúng ta sẽ xét tập hợp các dãy phần tử có dạng:
(x1, x2,.... xn) ∈ D₁ x D₂ x ... x Dn (1)
Trong đó D₁, D₂, ..., Dn là các tập hợp thuộc miền tìm kiếm của bài toán.
Các dãy (1) sẽ luôn được phép mở rộng ra để tìm nghiệm của bài toán gốc. Chú ý số lượng các tập hợp Di và bản thân mỗi tập hợp này có thể rất lớn, do đó việc tìm kiếm vét cạn trên toàn bộ các dãy (1) là không khả thi. Do vậy cần thiết lập thuật toán duyệt quay lui để giảm thiểu tối đa việc tìm kiếm trên các dãy (1).
Chúng ta sẽ định nghĩa tập hợp Sk ∈ Dk theo yêu cầu sau:
Sk = {x ∈ Dk, dãy (x1, x2,.... xk-1) có thể mở rộng thành (x1, x2,.... xk)} (2)
Ý nghĩa của việc đưa Sk vào để giảm bớt tối đa khả năng tìm kiếm Xk. Như vậy, với mỗi k, tập hợp Sk sẽ phụ thuộc vào các phần tử đã tìm được trước đó (x1, x2,.... xk-1). Sk do đó sẽ nhỏ đi đáng kể so với tập hợp gốc Dk.
Bài toán duyệt quay lui có 2 phương án: (i) tìm tất cả các nghiệm và (ii) chỉ cần tìm đúng một nghiệm. Sau đây là thiết kế hàm đệ quy chính của thuật toán duyệt quay lui trên mô hình (1) và (2) và thực hiện bài toán tìm tất cả các nghiệm.
Mô hình tổng quát duyệt quay lui sử dụng đệ quy như sau:
1 def Backtracking([x1, x2,.... xk-1], k):
2 if (x1, x2,.... xk-1) là nghiệm:
3 Lưu và thông báo nghiệm
4 Tính toán Sk theo (x1, x2,.... xk-1)
5 for xk in Sk: # Duyệt theo thứ tự của Sk
6 Backtracking([x1, x2,.... xk], k + 1)
Lệnh gọi hàm gốc như sau:
Backtracking([], 0)
Giải thích
– Vị trí xuất phát từ đầu là dãy rỗng và k = 0.
– Nếu trạng thái hiện thời (x1, x2,.... xk-1) là nghiệm của bài toán thì thông báo ngay.
– Tính toán lại Sk dựa trên trạng thái hiện thời (x1, x2,.... xk-1) tại dòng 4.
– Vòng lặp tại dòng 5 sẽ duyệt trên Sk để tìm phần tử đưa vào dãy và gọi tiếp hàm đệ quy cho bước tiếp theo tại dòng 6.
Lưu ý: Vòng lặp for tại dòng 5 sẽ thực hiện duyệt theo thứ tự các phần tử đang có của Sk. Như vậy, yêu cầu các tập hợp Dk phải được sắp xếp thứ tự trước.
(Trang 59)
| Mô hình tổng quát duyệt quay lui tổng quát quy định việc tìm trên các dãy số nguyên (x1, x2,.... xk) sử dụng lệnh gọi đệ quy để mô tả bước đi tiếp theo với k + 1, nếu không tìm được bước đi tiếp theo thì quay lui để tìm hướng đi khác. |
1. Trạng thái “quay lui” của thuật toán trên nằm ở đâu?
2. Có cách nào đem được tất cả các nghiệm từ thuật toán trên được không? Nếu có thì làm cách nào?
3. Bài toán sinh xâu nhị phân
| Hoạt động 3 Thiết kế chương trình sinh tất cả các dãy nhị phân Thực hiện, trao đổi, thảo luận thiết kế chương trình sinh tất cả các dãy nhị phân độ dài n bằng kĩ thuật quay lui. |
Chúng ta sẽ áp dụng thuật toán duyệt quay lui đã được mô tả trong Hoạt động 2 để giải bài toán tìm tất cả các dãy nhị phân độ dài n. Nghiệm của bài toán sẽ được lưu trong một dãy dạng A=A[0], A[ 1], ...,A[n - 1]. Chúng ta sẽ thiết lập trước dãy A bao gồm n số 0 và tiến hành tìm và gán từng phần tử vào A. Miền xác định ở đây là các tập hợp D = {0, 1}. Vì phần tử A[k] không phụ thuộc vào các phần tử phía trước nên ta luôn có Sk = {0, 1}. Thuật toán được mô tả bằng hàm đệ quy như sau:
Chương trình 1.
1 def genBinary(A,k):
2 if k == n:
3 print(A)
4 else:
5 for i in range(2):
6 A[k] = i
7 genBinary(A,k + 1)
Lưu ý: Lệnh nạp dữ liệu mới sau mỗi bước đi tiếp là dòng 6. Vì dãy A đã được thiết lập từ trước có đủ n phần tử nên tại bước này chỉ là lệnh gán giá trị A[k] = i. Muốn chạy chương trình gốc, thiết lập n và dãy A gồm n số 0, sau đó gọi hàm chính như sau:
1 n = 4
2 A = *n
3 genBinary(A,0)
(Trang 60)
Chúng ta ta thiết lập thêm phương án nữa cho thuật toán trên, khi dãy gốc ban đầu đặt là rỗng A = []. Chú ý các thay đổi quan trọng so với chương trình trên tại dòng 6 và 8 của chương trình 2 dưới đây. Vì A sẽ được bổ sung dần, nên dòng 6 sẽ phải dùng phương thức append(). Sau khi kết thúc lệnh gọi đệ quy tại dòng 7, khi quay lui cần xoá phần tử đã nhập từ bước trước nên cần lệnh pop() tại dòng 8.
Chương trình 2.
1 def genBinary(A,k):
2 if k == n:
3 print(A)
4 else:
5 for i in range(2):
6 A.append(i)
7 genBinary(A,k + 1)
8 A.pop()
Lời gọi hàm ở Chương trình chính sẽ như sau:
1 n = 4
2 genBinary([],0)
| Bài toán sinh tất cả các xâu nhị phân có thể giải quyết bằng mô hình của thuật toán quay lui tổng quát. |
1. Trong chương trình 1, động tác “quay lui” nằm ở đâu?
2. Giải thích ý nghĩa của lệnh A.pop() tại dòng 8 của chương trình 2. Vì sao lệnh này không có trong chương trình 1?
LUYỆN TẬP
1. Sửa các chương trình trên bổ sung thêm chức năng: sau khi in ra tất cả các xâu nhị phân thì thông báo tổng
số nghiệm.
2. Viết chương trình sinh tất cả các xâu (hoặc dãy) bao gồm n kí tự dạng "R","G" và "B".
VẬN DỤNG
1. Viết chương trình sinh tất cả các số hex (hệ đếm 16) có 3 chữ số.
2. Viết chương trình sinh xâu nhị phân thực sự có độ dài n, tức là kết quả in ra phải là các xâu kí tự chứ không phải là danh sách (list) như trong các chương trình trên.
Các Bài Học Khác
Chuyên đề học tập Tin học 11 - Bài 14: Thực Hành Kĩ Thuật Duyệt Quay Lui - Sử dụng kĩ thuật quay lui giải bài toán in ra tất cả các dạng mạch đơn của ADN và sinh ra các câu văn từ tập hợp từ vựng.
Xem thêm ⟶
Chuyên đề học tập Tin học 11 - Bài 15: Bài Toán Xếp Hậu - Thực hiện chương trình giải bài toán xếp Hậu trên bàn cờ bằng kĩ thuật duyệt quay lui.
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn