Nội Dung Chính
(Trang 28)
| Sau bài này em sẽ:
|
|
Trò chơi tìm bi giả Có 5 viên bi giống hệt nhau, biết rằng trong các viên bi này có một viên bi giả và viên bi giả này nặng hơn các viên bi còn lại. Chỉ với một cái cân thăng bằng, em hãy tìm ra viên bi đó. Cân ít nhất bao nhiêu lần cân để tìm ra bi giả? |
Hình 6.1. Cân thăng bằng |
1. Ý tưởng chia để trị
| Hoạt động 1 Tìm hiểu ý tưởng của kĩ thuật chia để trị để giải một bài toán 1. Hãy trình bày cách giải bài toán tìm bi giả với 5 viên bi. 2. Trường hợp tổng quát có n viên bi cách làm như thế nào? 3. Ý tưởng chia để trị của bài toán tìm bi giả sẽ được thể hiện như thế nào? |

- Với 5 viên bi, lần cân đầu tiên chúng ta lấy 4 viên bi, đặt 2 viên bi ở hai bên cân.
Trường hợp 1. Nếu cân thăng bằng thì viên bi không được cân bị lỗi, còn lại là bi giả. Như vậy, sau lần cân thứ nhất ta tìm được bi giả.
Trường hợp 2. Nếu cân bị lệch, ta sẽ xác định được bên nặng hơn chứa bi giả. Lấy hai viên bi ở bên nặng hơn và cân mỗi bên một viên, ta sẽ xác định được viên bi giả. Như vậy sau lần cân thứ hai ta tìm được bi giả.
- Với n viên bi.
- Nếu n lẻ, n = 2k + 1, sau lần cân thứ nhất với mỗi bên k viên, hoặc tìm thấy ngay viên bi giả, hoặc biết bên nào có chứa bi giả và tiếp tục cân với k viên bi đó.
- Nếu n chẵn, n = 2k, sau lần cân thứ nhất, ta tìm được k viên bi chứa viên bi giả.
Tổng quát sau mỗi lần cân, bài toán với n viên bi sẽ dẫn đến bài toán với [n/2] viên bi ([x] là phần nguyên của x). Khi bài toán dẫn đến con hai hoặc ba viên bi thì chỉ cần một lần cân nữa sẽ tìm được viên bi giả.
Ý tưởng chia để trị là bài toán ở trên được gọi là chia để trị. Tùy bài toán gốc luôn chia thành các bài toán có kích thước nhỏ hơn, ở đây là [n/2]. Khi số bi còn lại là 2 thì bài toán rất đơn giản có thể giải quyết ngay, đó là trị. Sau khi trị xong, kết hợp lại cả quá trình để tổng hợp kết quả chung sẽ giải quyết được bài toán gốc.
(Trang 29)
Chia để trị (Divide and Conquer) là một kĩ thuật rất quan trọng trong thiết kế thuật toán và chương trình. Gồm ba bước như sau:
Bước 1: Chia (Divide) Chia bài toán ban đầu (phức tạp) thành hai hoặc nhiều bài toán con (đơn giản hơn). Các bài toán con này có cùng dạng với bài toán ban đầu hoặc có liên quan với nhau. Mỗi bài toán con có thể được giải quyết một cách độc lập. Áp dụng tiếp tục kĩ thuật chia để trị để chia một bài toán con thành các bài toán con đơn giản hơn nữa (một cách đệ quy) và cứ như thế cho đến khi tất cả các bài toán con đủ đơn giản, có thể được giải quyết một cách dễ dàng.
Bước 2: Trị (Conquer) Giải quyết các bài toán con, kết quả là các lời giải của các bài toán con.
Bước 3: Kết hợp (Combine) Kết hợp các lời giải của các bài toán con để có được lời giải của bài toán ban đầu.
Nếu bài toán ban đầu được chia thành các bài toán con có cùng dạng với nó thì quá trình phân chia và giải quyết các bài toán này là quá trình đệ quy.
Thuật toán chia để trị. Gọi P là bài toán cần giải quyết. Hàm chiaĐểTrị(P) giải quyết bài toán P dùng kĩ thuật chia để trị.
def chiaDeTri(P):
if P là bài toán đủ đơn giản:
loi_giai = <giải quyết bài toán P>
else:
<Chia bài toán P thành các bài toán con> # Chia
<Gọi tapbCon là tập các bài toán con>
<Gọi tapLGcon là tập các lời giải của các bài toán con>
for btcCon in tapbCon:
lgiCon = chiaDeTri(btcCon)
<Ghi nhận lgiCon vào tapLgiCon> # Trị
loi_giai = <kết hợp các lời giải của tập tapLgiCon> # Kết hợp
return loi_giai
Gọi hàm ChiaDeTri(P) với P là bài toán ban đầu cần giải quyết.
Sơ đồ ý tưởng chia để trị như sau:
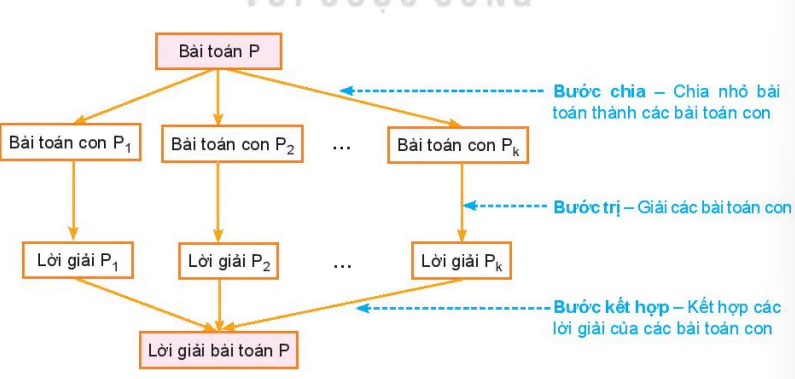
Hình 6.2. Sơ đồ ý tưởng chia để trị
Bài toán P
Bài toán P1
Bài toán P2
...
Bài toán Pk
Bước chia — Nhỏ bài toán thành các bài toán con
Lời giải P1
Lời giải P2
...
Lời giải Pk
Bước trị — Giải các bài toán con
Lời giải bài toán P
Bước kết hợp — Kết hợp các lời giải của các bài toán con
(Trang 30)
| Kĩ thuật chia để trị là phương pháp thiết kế thuật toán theo 3 giai đoạn: chia (divide), trị (conquer) và kết hợp (combine). Bài toán gốc sẽ được chia thành các bài toán con với kích thước nhỏ hơn. Sau đó sẽ trị (giải quyết) các bài toán con với kích thước nhỏ hơn. Cuối cùng kết hợp các kết quả để giải quyết bài toán ban đầu. Kĩ thuật chia để trị thường sử dụng kĩ thuật đệ quy ở bước chia (Divide) và bước trị (Conquer). |
![]()
1. Với n = 9 bài toán tìm bi giả cần tối đa bao nhiêu lần cân?
2. Mô tả bước "kết hợp" của bài toán 9 viên bi trên.
2. Thuật toán tìm kiếm nhị phân
| Hoạt động 2 Tìm hiểu kĩ thuật chia để trị thông qua tìm kiếm nhị phân Quan sát lại một lần nữa thuật toán tìm kiếm nhị phân trên dãy các phần tử đã sắp xếp và liên hệ với phương pháp chia để trị. |
![]()
Bài toán gốc của tìm kiếm nhị phân như sau:
Cho trước dãy A các số gồm n phần tử đã được sắp xếp theo thứ tự tăng dần: A[0] ≤ A[1] ≤... ≤ A[n - 1].
Cho trước giá trị cần tìm K. Cần tìm chỉ số i của dãy A sao cho A[i] = K. Nếu tìm thấy trả về i, nếu không thấy trả về –1.
Thuật toán tìm kiếm nhị phân được mô tả bởi hàm binarySearch(A, left, right, K) như sau:
1 def binarySearch(A, left, right, K):
2 if left >= right:
3 mid = (left + right)//2
4 if A[mid] == K:
5 return mid
6 elif A[mid] < K:
7 return binarySearch(A, mid + 1, right, K)
8 else:
9 return binarySearch(A, left, mid - 1, K)
10 else:
11 return -1
– Dòng lệnh 2 là điều kiện để thực hiện lời gọi đệ quy của chương trình. Hàm tìm kiếm chỉ thực hiện khi left ≤ right.
– Dòng 3 có nhiệm vụ chia bài toán tìm kiếm thành hai bài toán con: tìm kiếm bên trái và bên phải. Đây chính là bước Chia (Divide) của kĩ thuật chia để trị.
(Trang 31)
– Các dòng 7 và 9 thực hiện lệnh gọi đệ quy tương ứng với các nửa bên phải và nửa trái của dãy. Các lệnh này phụ thuộc vào lệnh tại dòng 3. Đây chính là bước Trị (Conquer) của kĩ thuật chia để trị.
– Khi thực hiện xong các dòng 7, 9 thì bài toán đã được giải xong. Ở đây bước Kết hợp (Combine) sẽ được tự động thực hiện ngay sau khi gọi đệ quy.
| Thuật toán tìm kiếm nhị phân là một triển khai của kĩ thuật chia để trị của bài toán tìm kiếm trên dãy các phần tử đã sắp xếp. |
![]()
1. Trong thuật toán tìm kiếm nhị phân trên, phần cơ sở là các lệnh nào?
2. Mô tả các bước thực hiện thuật toán tìm kiếm nhị phân khi left = right.
| Hoạt động 3 Đánh giá độ phức tạp thời gian của thuật toán tìm kiếm nhị phân Đọc, quan sát phân tích sau để biết được tính vượt trội của tìm kiếm nhị phân với tìm kiếm tuần tự, biết được vai trò của kĩ thuật chia để trị trong thiết kế thuật toán. |

Gọi T(n) là thời gian thực hiện thuật toán tìm kiếm nhị phân trong chương trình trên, n là độ dài dãy A.
– Nếu n = 1, tức là left = right. Nếu A[left] = K thì sẽ thực hiện ngay các lệnh tại dòng 5 và dừng chương trình. Nếu A[left] ≠ K thì sẽ gọi tiếp đệ quy tới các dòng 7 hoặc 9 nhưng sẽ trả về ngay – 1. Vậy trong mọi trường hợp tổng số phép toán thực hiện khi n = 1 chỉ là hằng số, ta có T(1) = O(1).
– Nếu n > 1, nếu A[mid] ≠ K thì chương trình sẽ gọi đệ quy tại các lệnh 7 hoặc 9, các lệnh gọi đệ quy này sẽ chạy trên dãy có kích thước n/2. Như vậy, trong mọi trường hợp chúng ta có công thức sau cho trường hợp tổng quát:
T(n) = T(n/2) + O(1).
Vậy không mất tổng quát có thể giả thiết tồn tại hằng số C sao cho:
T(1) = C (1)
T(n) = T(n/2) + C (2)
Từ các công thức (1), (2) có thể chứng minh được T(n) = O(logn).
Để tham khảo chúng ta sẽ chứng minh công thức T(n) = O(logn) trong trường hợp n = 2k, k = log2n.
Theo công thức (2) ta có:
T(n) = T(2k) = T(2k-1) + C
= T(2k-2) + C + C = T(2k-2) + 2C = ...
= T(20) + kC //theo công thức (1)
= (k + 1)C
= C.k + C = C.log2n + C = O(log2n).
(Trang 32)
| Thuật toán tìm kiếm nhị phân có độ phức tạp thời gian O(logn), tốt hơn hẳn của tìm kiếm tuần tự với thời gian chạy là O(n). |

1. Tìm chính xác số phép toán đơn cần thực hiện trong thuật toán tìm kiếm nhị phân nếu dãy gốc chỉ có 1 phần tử.
2. Tìm số phép toán đơn cần thực hiện trong thuật toán trên nếu dãy có 2 phần tử.

LUYỆN TẬP
1. Viết chương trình hoàn chỉnh nhập dãy số từ bàn phím, các số cách nhau bởi dấu cách. Sau đó, nhập số K bất kì từ bàn phím và thực hiện việc tìm kiếm số K trong dãy trên. Nếu tìm thấy thì trả lại chỉ số của phần tử có giá trị K, ngược lại trả về –1.
2. Cho trước danh sách gồm có tên, điểm thi và được sắp xếp theo thứ tự tăng dần của điểm thi, ví dụ danh sách: [["Binh", 7.5], ["Hoa", 8], ["An", 9], ["Quang", 10]]. Viết chương trình nhập một điểm số và tìm tên học sinh có điểm thi bằng điểm số đã nhập, nếu không tìm thấy thì thông báo "không có".

VẬN DỤNG
1. Phương án không đệ quy của thuật toán tìm kiếm nhị phân có phải là chia để trị không?
2. Em hãy viết chương trình cài đặt các thuật toán tìm kiếm tuần tự và nhị phân rồi tiến hành đo thời gian thực trên máy tính với hai thuật toán này. Thực hiện kiểm thử với các bộ dữ liệu n = 10, 20, 50, 100 và ghi vào bảng để so sánh thời gian chạy giữa hai thuật toán tìm kiếm này.
3. Cho trước giá trị (số nguyên) n cần tìm bậc hai của số tự nhiên n cho trước, người ta đã thiết lập hàm sau với ý tưởng gần tương tự thuật toán tìm kiếm tuần tự như sau:
1 def floorSqrt(n):
2 k = 1
3 while k*k <= n:
4 k = k + 1
5 return k - 1
Hãy thiết kế thuật toán tìm kiếm số nguyên lớn nhất không vượt quá căn bậc hai của n bằng kĩ thuật chia để trị.








































































Bình Luận
Để Lại Bình Luận Của Bạn