Nội Dung Chính
(Trang 37)
| Sau bài này em sẽ:
|
|
Cho một dãy số A bất kì. Để xác định một số C cho trước xuất hiện trong dãy A bao nhiêu lần thì làm thế nào? |
NHIỆM VỤ 1
Tìm số lần lặp của một giá trị trên dãy đã sắp xếp.
Cho trước dãy số A đã sắp xếp theo thứ tự tăng dần, cho trước hằng số C. Hãy tìm xem trong dãy trên có bao nhiêu số hạng bằng C. Ví dụ nếu A =, C = 2 thì kết quả cần tìm là 4.
Hướng dẫn:
Ý tưởng: thuận toán tiên, nhận xét rằng bài tập này có thể dễ dàng giải bằng phương pháp tìm kiếm tuần tự đã quen biết. Gọi count là số lần xuất hiện của C trong dãy. Thực hiện tìm kiếm tuần tự với C, mỗi lần tìm thấy C, tăng biến count lên 1.
Chương trình đơn giản như sau:
1 def countNum(A,C):
2 count = 0
3 for i in range(len(A)):
4 if A[i] == C:
5 count = count + 1
6 return count
Thuật toán trên có một vòng lặp tại dòng 3 thực hiện n lần (n = len(A)), do đó thời gian chạy là O(n).
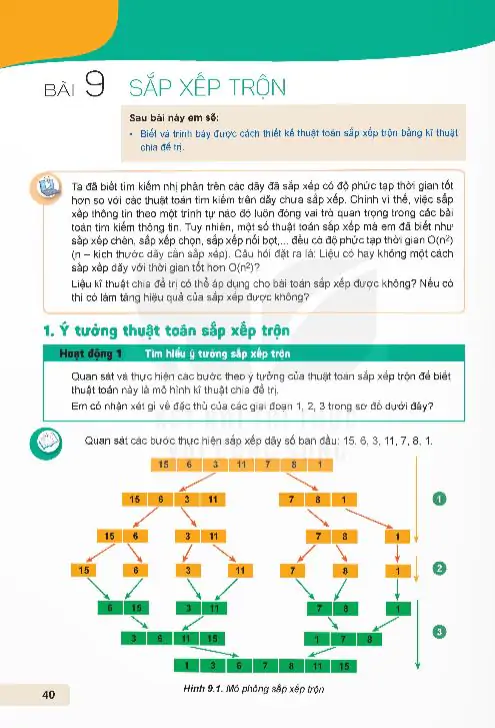
Bây giờ chúng ta sẽ thiết lập lời giải bài toán trên theo kĩ thuật chia để trị. Vì dãy ban đầu đã được sắp xếp theo thứ tự tăng dần nên ý tưởng của lời giải là theo cách làm của thuật toán tìm kiếm nhị phân. Gọi n là kích thước của dãy số gốc.
Chúng ta sẽ thiết lập hàm tìm kiếm dạng countNum(A, left, right, C) để thực hiện tìm kiếm số lần lặp của C trong khoảng chỉ số từ left đến right.
Trường hợp left > right (dãy ban đầu rỗng) thì lập tức trả về 0.
Xét trường hợp left <= right. Gọi mid = (left + right)/2 là chỉ số phần tử ở giữa dãy đang tìm. Việc tìm kiếm tiếp sẽ theo các bước sau:
Nếu A[mid] = C thì tìm số các phần tử bằng C bằng cách duyệt các phần tử trước và sau mid.
Nếu A[mid] < C thì cần tìm tiếp trong khoảng nửa dãy bên phải từ mid + 1 đến right.
Nếu A[mid] > C thì cần tìm tiếp trong khoảng nửa dãy bên trái từ left đến mid - 1. Chương trình hoàn chỉnh có thể như sau:
1 def countNum(A,left,right,C):
2 if left > right:
3 return 0
4 else:
5 mid = (left+right)//2
6 if A[mid] == C:
7 start = mid
8 while start >= left and A[start] == C:
9 start = start - 1
10 end = mid
11 while end <= right and A[end] == C:
12 end = end + 1
13 return end - start - 1
14 elif A[mid] < C:
15 return countNum(A,mid+1,right,C)
16 else:
17 return countNum(A,left,mid-1,C)
Lệnh gọi đệ quy của hàm tìm kiếm là:
countNum(A, 0, len(A) - 1, C)
(Trang 39)
Nhận xét:
- Chương trình trên hoàn toàn tương tự thuật toán tìm kiếm nhị phân, điểm khác biệt tại các dòng lệnh từ 6 đến 13 khi xử lí trường hợp A[mid] = C.
- Các dòng 2, 3 là phần cơ sở của đệ quy.
- Việc “chia” được thực hiện tại dòng 5. Các lệnh tiếp theo chính là “trị”. Bài toán này khá đơn giản nên sau khi “trị” sẽ thu được luôn kết quả.
- Trong hầu hết các trường hợp việc xử lí tại dòng 6 đến dòng 13 sẽ mất O(1) thời gian. Trong một số trường hợp xấu nhất, ví dụ dãy ban đầu bao gồm tất cả các số C thì việc xử lí A[mid] = C sẽ mất O(n) thời gian.
LUYỆN TẬP
Chỉnh sửa nâng cấp chương trình của nhiệm vụ thực hành để đưa ra kết quả là vùng các phần tử có giá trị bằng C của dãy gốc. Tức là yêu cầu đưa ra chỉ số đầu, chỉ số cuối và số lượng phần tử của vùng có giá trị bằng C.
Ví dụ nếu A = [0, 1, 2, 2, 2, 2, 4, 5, 5, 6], C = 2, thì kết quả trả lại là 2, 5, 4.
VẬN DỤNG
1. Cho một dãy số bất kì (chưa được sắp xếp) và một số K, hãy tìm số lần xuất hiện của K trong dãy số trên. Yêu cầu sử dụng phương pháp chia để trị.
2. Cho một dãy số nguyên được sắp xếp theo thứ tự tăng dần, hãy tìm một vị trí thứ i trong dãy sao cho phần tử thứ i có giá trị bằng I.
3. Cho trước dãy số A đã sắp xếp theo thứ tự tăng dần, cho trước hằng số C. Cần thiết lập hai hàm sau bằng kĩ thuật chia để trị:
- Hàm firstInd(A, left, right, C) sẽ tìm chỉ số của phần tử đầu tiên của dãy A có giá trị bằng C. Nếu không thấy sẽ trả về -1.
- Hàm lastInd(A, left, right, C) sẽ tìm chỉ số của phần tử cuối cùng của dãy A có giá trị bằng C. Nếu không thấy sẽ trả về -1.
Từ hai hàm đã thiết kế trên, đưa ra một cách giải khác cho bài toán trong nhiệm vụ 1. Lời giải này có độ phức tạp O(logn).
Các Bài Học Khác
Chuyên đề học tập Tin học 11 - Bài 9: Sắp Xếp Trộn - Cách thiết kế thuật toán sắp xếp trộn bằng kĩ thuật chia để trị, bao gồm thuật toán trộn hai dãy.
Xem thêm ⟶
Chuyên đề học tập Tin học 11 - Bài 10: Thực Hành Giải Toán Bằng Kĩ Thuật Chia Để Trị - Thiết kế và viết chương trình giải bài toán đếm số cặp nghịch đảo trong dãy số bằng kĩ thuật chia để trị.
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn