Nội Dung Chính
(Trang 40)
| Sau bài này em sẽ:
|
|
Ta đã biết tìm kiếm nhị phân trên các dãy đã sắp xếp có độ phức tạp thời gian tốt hơn so với các thuật toán tìm kiếm trên dãy chưa sắp xếp. Chính vì thế, việc sắp xếp thông tin theo một trình tự nào đó luôn đóng vai trò quan trọng trong các bài toán tìm kiếm thông tin. Tuy nhiên, một số thuật toán sắp xếp mà em đã biết như sắp xếp chọn, sắp xếp chèn, sắp xếp nổi bọt,... đều có độ phức tạp thời gian O(n²) (n = kích thước dãy cần sắp xếp). Câu hỏi đặt ra là: Liệu có hay không một cách sắp xếp dãy với thời gian tốt hơn O(n²)? Liệu kĩ thuật chia để trị có thể áp dụng cho bài toán sắp xếp được không? Nếu có thì có làm tăng hiệu quả của sắp xếp được không? |
1. Ý tưởng thuật toán sắp xếp trộn
| Hoạt động 1 Tìm hiểu ý tưởng thuật toán sắp xếp trộn Quan sát và thực hiện các bước theo ý tưởng của thuật toán sắp xếp trộn để biết thuật toán này là mô hình kĩ thuật chia để trị. Em có nhận xét gì về đặc thù của các giai đoạn 1, 2, 3 trong sơ đồ dưới đây. |
![]()
Quan sát các bước thực hiện sắp xếp dãy số ban đầu: 15, 6, 3, 11, 7, 8, 1.
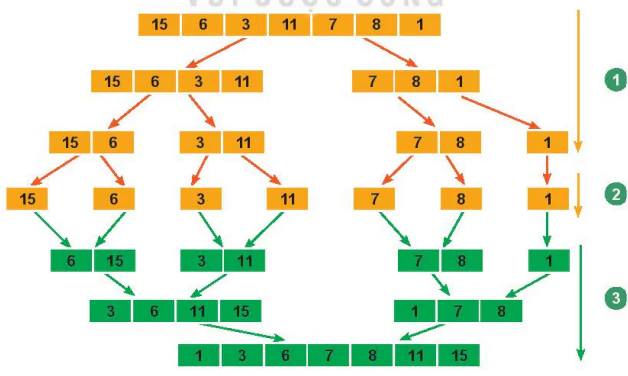
Hình 9.1. Mô phỏng sắp xếp trộn
15 6 3 11 7 8 1
15 6 3 11 7 8 1
15 6 3 11 7 8 1
15 6 3 11 7 8 1
6 15 3 11 7 8 1
3 6 11 15 1 7 8
1 3 6 7 8 11 15
(Trang 41)
Giai đoạn 1. Từ dãy gốc ban đầu chúng ta tách đôi làm hai dãy con, mỗi dãy con có kích thước bằng 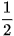 kích thước của dãy gốc. Quá trình này chính là bước Chia (divide) của kĩ thuật chia để trị.
kích thước của dãy gốc. Quá trình này chính là bước Chia (divide) của kĩ thuật chia để trị.
Giai đoạn 2. Khi tất cả các dãy con thu được đều chỉ còn một phần tử. Tất cả các dãy này hiển nhiên đều đã được sắp xếp đúng. Vậy việc trị đã xong. Đây chính là bước Trị (conquer) tương ứng của chiến lược chia để trị.
Giai đoạn 3. Từ các dãy đã sắp xếp xong, chúng ta sẽ trộn chúng lại với nhau, mỗi lần trộn hai dãy đã sắp xếp để tạo thành một dãy lớn hơn cũng được sắp xếp đúng. Quá trình trộn sẽ kết thúc khi nhận được đúng một dãy chính là dãy ban đầu nhưng đã sắp xếp xong. Đây chính là quá trình Kết hợp (combine) tương ứng của kĩ thuật chia để trị.
Ý tưởng của thuật toán sắp xếp trộn được thực hiện qua 3 bước: Chia nhỏ dãy gốc thành các dãy con với kích thước nhỏ (bằng 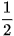 dãy ban đầu), tiếp tục cho đến khi nhận được các dãy con đã sắp xếp đúng thì tiến hành trộn các dãy này để nhận được kết quả cuối cùng. Các bước trên chính là kĩ thuật chia để trị. dãy ban đầu), tiếp tục cho đến khi nhận được các dãy con đã sắp xếp đúng thì tiến hành trộn các dãy này để nhận được kết quả cuối cùng. Các bước trên chính là kĩ thuật chia để trị. |
![]()
1. Hãy thực hiện thao tác trộn hai dãy sau: B = 1, 4, 7; C = 2, 3, 6.
2. Thực hiện sắp xếp dãy 3, 2, 7, 1, 6, 5 theo các bước tương tự trên.
2. Mô tả thuật toán sắp xếp trộn
| Hoạt động 2 Tìm hiểu các bước thực hiện sắp xếp trộn Cùng thực hiện các bước cụ thể triển khai ý tưởng và cài đặt chương trình cho thuật toán sắp xếp trộn. |
![]()
Từ các ý tưởng của thuật toán sắp xếp trộn trong hoạt động trước, chúng ta sẽ tìm hiểu và thiết lập các thuật toán và chương trình có liên quan.
a) Thuật toán trộn hai dãy (merge algorithm)
Giả sử cho trước hai dãy đã được sắp thứ tự B và C có phần tử lần lượt là m, n. Thuật toán merge(B, C) sẽ thực hiện “trộn” hai dãy B và C đưa kết quả vào dãy A. Quy trình trộn này rất tự nhiên và được minh họa trong sơ đồ sau:
Thiết lập sẵn dãy A bao gồm m + n phần tử. Chúng ta cần 3 biến chỉ số i, j, k chạy trên các dãy B, C và A. Tại mỗi bước lặp, so sánh B[i] và C[j], nếu B[i] < C[j] thì đưa B[i] vào vị trí A[k], tăng i lên 1 đơn vị. Ngược lại, đưa C[j] vào A[k], tăng j lên 1 đơn vị. Sau mỗi bước tăng sẽ tăng k lên 1 đơn vị. Quá trình này liên tục cho đến khi hoặc i hoặc j vượt quá trị cuối. Khi đó phần dãy còn lại sẽ được đưa nốt vào A. Do tính chất đã sắp xếp của B, C nên ta thu được xong được sắp xếp và là kết quả của phép trộn B và C. Một đặc tính quan trọng của thuật toán này là thời gian chạy O(m + n) vì chỉ duyệt trên chiều dài của B và C cộng lại.
(Trang 42)
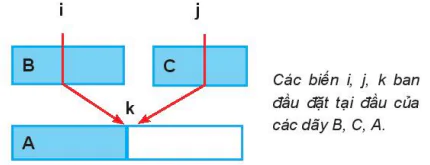
Hình 9.2. Trộn hai dãy B và C
Các biến i, j, k ban đầu đặt tại đầu của các dãy B, C, А.
Thuật toán 1. Thuật toán trộn hai dãy (đã được sắp xếp).

1 def merge(B,C):
2 m = len(B)
3 n = len(C)
4 A = * (m+n)
#Thiết lập dãy A bao gồm m+n số 0
5 i = j = k = 0
6 while i < m and j < n: Bắt đầu duyệt tại đây.
7 if B[i] < C[j]:
8 A[k] = B[i]
9 i = i + 1
10 else:
11 A[k] = C[j]
12 j = j + 1
13 k = k + 1
14 if i == m:
15 while j < n: Nếu đã duyệt xong B thì đưa nốt phần còn lại của C vào A.
16 A[k] = C[j]
17 j = j + 1
18 k = k + 1
19 else:
20 while i < m: Nếu đã duyệt xong C thì đưa nốt phần còn lại của B vào А.
21 A[k] = B[i]
22 i = i + 1
23 k = k + 1
24 return A
b) Thuật toán sắp xếp trộn (mergeSort)
Thuật toán sắp xếp trộn được mô tả bởi hàm mergeSort(A) trong chương trình sau. Các dòng lệnh 2, 3 là phần cơ sở của đệ quy. Dòng lệnh 5 thực hiện chia dãy A làm hai phần có kích thước hơn kém nhau không quá 1. Các lệnh gọi đệ quy 6, 7 chính là phép trị để nhận được hai dãy đã sắp xếp xong có kích thước nhỏ hơn. Lệnh 8 sử dụng hàm trộn merge(B, C) thực hiện việc kết hợp để nhận được kết quả cuối cùng.
Thuật toán 2. Thuật toán sắp xếp trộn.
1 def mergeSort(A):
2 if len(A) <= 1:
3 return A
4 else:
5 k = len(A)//2
6 B = mergeSort(A[:k])
7 C = mergeSort(A[k:])
8 return merge(B, C)
Đoạn chương trình sau sẽ thực hiện sắp xếp dãy A và đưa kết quả đã sắp xếp vào dãy B. Lời gọi hàm đệ quy là:
1 A = [2, 1, 10, 0, -7, -20, 19, 100, -3, -2, 9, 11]
2 B = mergeSort(A)
Lưu ý: Có nhiều phương án thực hiện sắp xếp khác nhau, trên đây chỉ mô tả một trong các phương án cài đặt của thuật toán.
| Thuật toán sắp xếp trộn sẽ bao gồm một hàm mergeSort(), hàm này sẽ tiến hành các bước chính của thuật toán và gọi hàm trộn hai dãy đã sắp xếp merge() khi thực hiện bước kết hợp. |
![]()
1. Trong chương trình 1 (trộn hai dãy B, C), vòng lặp tại dòng 6 có nhiều nhất là bao nhiêu bước lặp?
2. Mô tả các bước thực hiện chương trình 2 nếu dãy gốc A chỉ có một phần tử.
3. Đánh giá thuật toán sắp xếp trộn
| Hoạt động 3 Tìm hiểu đánh giá độ phức tạp thời gian của sắp xếp trộn Phân tích, trao đổi, thảo luận về thuật toán và thiết lập chương trình hoàn chỉnh giải bài toán. |
![]()
Phân tích: Gọi T(n) là thời gian chạy của thuật toán sắp xếp trộn.
Với n = 1, dòng lệnh 2 trả lại ngay dãy gốc A, do đó T(1) = 1.
Trường hợp tổng quát:
– Tại bước chia (dòng 5), cần O(1) thời gian để thực hiện.
– Các dòng 6, 7 sẽ mất 2T(n/2) thời gian.
– Dòng lệnh 8 thực hiện trộn hai dãy với thời gian O(n).
Tổng kết lại chúng ta các công thức truy hồi thời gian T(n).
T(1) = 1
T(n) = 2T(n/2) + O(n), n > 1 (1)
Không mất tổng quát, giả sử tồn tại hằng số C > 0 sao cho:
T(n) = 2T(n/2) + Cn, n > 1 (2)
(Trang 44)
Các công thức (1), (2) được gọi là công thức truy hồi để tính độ phức tạp thời gian T(n) của thuật toán trộn.
Người ta tính được: T(n) = O(nlogn).
| Thuật toán sắp xếp trộn sử dụng kĩ thuật chia để trị có độ phức tạp thời gian O(nlogn), bậc thời gian này là tốt hơn hẳn các thuật toán sắp xếp mà chúng ta đã biết (sắp xếp chèn, sắp xếp chọn và sắp xếp nổi bọt). |

1. Tính thời gian chạy của thuật toán sắp xếp trộn nếu các bước của thuật toán sắp xếp trộn với dãy A =.
2. Mô tả thực hiện các bước của thuật toán sắp xếp trộn với dãy A =. Trường hợp này T(4) sẽ được tính như thế nào

LUYỆN TẬP
1. Viết chương trình thực hiện công việc sau:
– Đọc dữ liệu nhập từ tệp văn bản Data.inp bao gồm hai dòng, mỗi dòng là một dãy các số nguyên đã được sắp xếp theo thứ tự tăng dần, các số cách nhau bởi dấu cách. Hai dãy này có thể không bằng nhau về kích thước.
– Chương trình sẽ thực hiện trộn hai dãy trên và đưa kết quả dãy được trộn ra tệp Data.out theo một hàng ngang.
2. Viết lại chương trình hoàn chỉnh thực hiện sắp xếp trộn với dãy A cho trước trên một tệp văn bản. Kết quả đưa ra màn hình.

VẬN DỤNG
1. Viết chương trình hoàn chỉnh nhập dãy số bất kì từ tệp văn bản, sau đó tiến hành sắp xếp dãy số này theo hai cách khác nhau, cách 1 là một trong các thuật toán sắp xếp đã biết, cách 2 là sắp xếp trộn. Độ thời gian chạy thực sự của hai cách trên, so sánh và kết luận ưu nhược điểm của sắp xếp trộn.
2. Viết lại thuật toán sắp xếp trộn theo cách thực hiện trực tiếp trên dãy số A cho trước, cụ thể như sau.
– Thủ tục trộn sẽ có dạng sau: merge(A,left,mid,right). Thủ tục này sẽ trộn hai phần đoạn của dãy A là A[left]...A[mid] và A[mid+1]...A[right]. Hai phần đoạn này phải được sắp xếp đúng trước đó.
– Thuật toán chính có dạng mergeSort(A, left, right) như sau:
1 def mergeSort(A, left, right):
2 if left < right:
3 mid = (left + right)//2
4 mergeSort(A, left, mid)
5 mergeSort(A, mid + 1, right)
6 merge(A, left, mid, right)
– Lệnh gọi hàm đệ quy là:
mergeSort(A, 0, len(A) - 1)






































































Bình Luận
Để Lại Bình Luận Của Bạn