Nội Dung Chính
(Trang 81)
| MỤC TIÊU Thực hành tính nguyên hàm và tính gần đúng tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình thang trong trường hợp hàm dưới dấu tích phân cho dạng bảng (tại một số mốc) hoặc cho bởi một đồ thị (mà ta không biết phương trình của nó) hoặc không có nguyên hàm dưới dạng hàm sơ cấp. |
1. TÍNH NGUYÊN HÀM VÀ TÍCH PHÂN VỚI PHẦN MỀM GEOGEBRA
Khởi động phần mềm GeoGebra
a) Tính nguyên hàm của hàm số
Để tính nguyên hàm của hàm số, ta dùng lệnh IntegralSymbolic (<hàm số>), kết quả sẽ được hiển thị ngay bên dưới.

Hình T1
| 1 | IntegralSymbolic(sin(2x))
|
| 2 | IntegralSymbolic
|
| 2 | IntegralSymbolic
|
| 2 | IntegralSymbolic(x sin(2x+1))
|
(Trang 82)
b) Tính tích phân
Để tính gần đúng tích phân, ta dùng lệnh NIntegral (<hàm số, giá trị đầu, giá trị cuối>), kết quả sẽ được hiển thị ngay bên dưới.
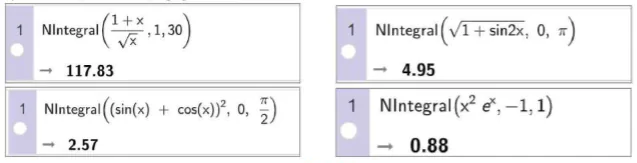
Hình T2
| 1 | NIntegral
| 1 | NIntegral
|
| 1 | NIntegral
| 1 | NIntegral
|
Chú ý. Nếu muốn sử dụng giao diện tiếng Việt, sau khi khởi động GeoGebra, chọn Options → Language → Vietnamese/Tiếng Việt. Khi đó, thay vì cú pháp lệnh tiếng Anh như trình bày ở trên, ta dùng cú pháp lệnh tiếng Việt tương ứng như trong bảng sau:
| Lệnh | Cú pháp lệnh tiếng Anh | Cú pháp lệnh tiếng Việt |
| Tính nguyên hàm | IntegralSymbolic (<hàm số>) | TíchPhân (<hàm số>) |
| Tính tích phân | NIntegral (<hàm số, giá trị đầu, giá trị cuối>) | TíchPhânXácĐịnh (<hàm số, giá trị đầu, giá trị cuối>) |
Thực hành 1. Sử dụng phần mềm GeoGebra, tính:
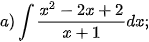
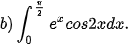
2. TÍNH GẦN ĐÚNG TÍCH PHÂN BẰNG PHƯƠNG PHÁP HÌNH THANG
Để tính tích phân 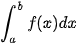 bằng định nghĩa, ta cần biết một nguyên hàm F(x) của f(x) trên đoạn [a; b]. Khi đó:
bằng định nghĩa, ta cần biết một nguyên hàm F(x) của f(x) trên đoạn [a; b]. Khi đó:
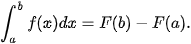
Tuy nhiên, nếu hàm số f(x) không có nguyên hàm dưới dạng hàm sơ cấp, chẳng hạn, người ta biết rằng
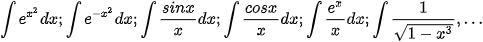
không phải là những hàm số sơ cấp, thì không thể dùng định nghĩa trên được. Tình huống tương tự xuất hiện khi f(x) cho bởi một đồ thị mà ta không biết phương trình của nó. Khi đó, ta cần tính xấp xỉ 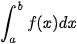 bằng các phương pháp số.
bằng các phương pháp số.
(Trang 83)
Phương pháp đơn giản nhất là phương pháp hình thang, có nội dung như sau:
Giả sử f(x) là hàm số liên tục trên đoạn [a; b]. Khi đó:
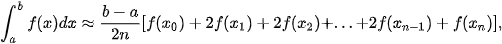
ở đó đoạn [a; b] được chia thành n đoạn con 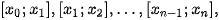 , mỗi đoạn có độ dài là
, mỗi đoạn có độ dài là 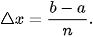
| Khi f(x) là hàm liên tục và không âm trên đoạn [a; b], ta có: Ý nghĩa hình học: Diện tích của hình phẳng giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b xấp xỉ với tổng diện tích của các hình thang con Đánh giá sai số: Người ta chứng minh được rằng nếu f"(x) liên tục trên đoạn [a; b] thì sai số |E| của phương pháp hình thang được đánh giá như sau: |
Hình T3
|
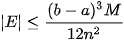 , trong đó
, trong đó 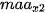
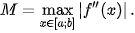
Thuật toán: Để tính xấp xỉ 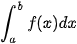 với độ chính xác không vượt quá số ε cho trước, ta thực hiện lần lượt các bước sau:
với độ chính xác không vượt quá số ε cho trước, ta thực hiện lần lượt các bước sau:
Bước 1. Tính f''(x) và tìm 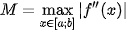
(hoặc đánh giá 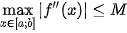 , nếu việc tìm chính xác là khó).
, nếu việc tìm chính xác là khó).
Bước 2. Với sai số ε cho trước, tìm số tự nhiên n (nhỏ nhất) sao cho
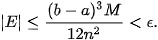
Bước 3. Chia đoạn [a; b] thành n đoạn con có độ dài bằng nhau và áp dụng công thức hình thang.
Ví dụ. Tính gần đúng 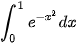 với độ chính xác nhỏ hơn 0,01.
với độ chính xác nhỏ hơn 0,01.
Giải
a) Ta có: 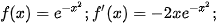
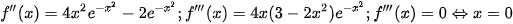 hoặc
hoặc 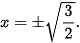
Ta có: 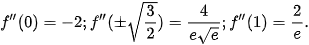
Do đó 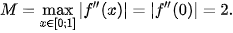
(Trang 84)
b) Ta cần tìm n sao cho
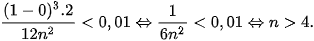
Do đó, ta chọn n = 5.
c) Chia đoạn [0; 1] thành 5 đoạn có độ dài bằng nhau là [0; 0,2], [0,2; 0,4], [0,4; 0,6], [0,6; 0,8], [0,8; 1].
Áp dụng công thức hình thang, ta có:
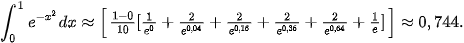
Thực hành 2. Sử dụng phương pháp hình thang, tính gần đúng 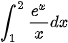 với độ chính xác 0,01.
với độ chính xác 0,01.
Vận dụng. Một thân cây dài 4,8 m được cắt thành các khúc gỗ dài 60 cm. Người ta đo đường kính của mỗi mặt cắt ngang và diện tích S của nó được ghi lại trong bảng dưới đây, ở đây x (cm) là khoảng cách tính từ đỉnh thân cây đến vết cắt.
| x (cm) | 0 | 60 | 120 | 180 | 240 | 300 | 360 | 420 | 480 |
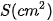 | 240 | 248 | 256 | 260 | 264 | 272 | 298 | 316 | 320 |
Tìm thể tích gần đúng của thân cây này.
Hướng dẫn.
Thể tích cần tính là 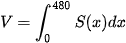 , trong đó S(x) là diện tích mặt cắt ngang tại vị trí cách đỉnh thân cây một khoảng x (cm). Sử dụng phương pháp hình thang để tính gần đúng tích phân này.
, trong đó S(x) là diện tích mặt cắt ngang tại vị trí cách đỉnh thân cây một khoảng x (cm). Sử dụng phương pháp hình thang để tính gần đúng tích phân này.
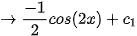
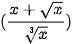
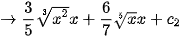
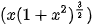
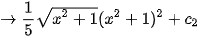
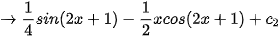
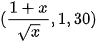
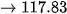
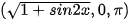
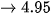
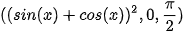
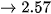
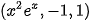
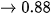
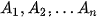 (H.T3).
(H.T3).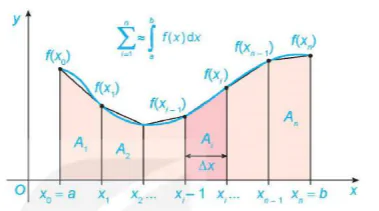
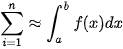
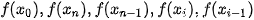

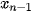
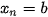


































































Bình Luận
Để Lại Bình Luận Của Bạn