Bài tập cuối chương V | Toán 12 - Tâp 2 | Chương V: Phương pháp tọa độ trong không gian - Lớp 12 - Kết Nối Tri Thức Với Cuộc Sống

(Trang 61)

A – TRẮC NGHIỆM

5.31. Trong không gian Oxyz, cho mặt phẳng (P): x − 2y – 3z + 1 = 0. Một vectơ pháp tuyến của mặt phẳng (P) có toạ độ là

A. (1; 2; 3).

B. (1;–2; 3).

C. (1; 2;–3).

D. (1;–2; –3).

5.32. Trong không gian Oxyz, phương trình mặt phẳng (P) đi qua điểm I(1; –1; 2) và nhận vectơ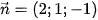

A. x – y + 2z + 1 = 0.

B. x – y + 2z – 6 = 0.

C. 2x + y – z – 1 = 0.

D. 2x + y – z + 1 = 0.

5.33. Trong không gian Oxyz, cho đường thẳng d: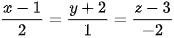. Một vectơ chỉ phương của đường thẳng d có toạ độ là

A. (1; –2; 3).

B. (2; 1; –2).

C. (2; 1; 2). 

D. (1; 2; 3).

5.34. Trong không gian Oxyz, cho đường thẳng d :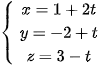. Một vectơ chỉ phương của đường thẳng d có toạ độ là
A. (1; –2; 3).

B. (2; 0; 0).

C. (2; 1; –1).

D. (2; 1; 1).

5.35. Trong không gian Oxyz, phương trình đường thẳng d đi qua I(2; –1; 1) và nhận vectơ 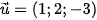làm một vectơ chỉ phương là

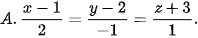
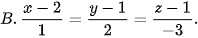
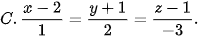
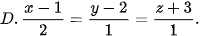
5.36. Trong không gian Oxyz, cho hai điểm A(-1; 0; –1), B(2; 1; 1). Phương trình đường thẳng AB là

.

.

.

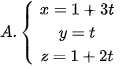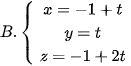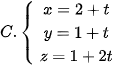
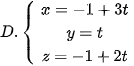5.37. Trong không gian Oxyz, phương trình đường thẳng d đi qua I(2; 1; −3) và vuông góc với mặt phẳng (P): x − 2y + z − 3 = 0 là

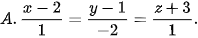
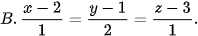
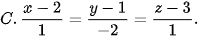
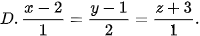
(Trang 62)

5.38. Trong không gian Oxyz, cho mặt cầu (S) :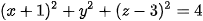. Toạ độ tâm I và bán kính R của (S) lần lượt là

A. I(1; 0; 3), R = 4.

B. I(1; 0; 3), R = 2.

C. I(-1; 0; 3), R = 2.

D. I(-1; 0; 3), R = 4.

5.39. Trong không gian Oxyz, cho mặt cầu (S): 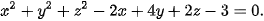Toạ độ tâm I và bán kính R của mặt cầu (S) lần lượt là

A. I(1; –2; –1), R = 3.

B. I(1, 2, 1), R = 9.

C. I(1; 2; 1), R = 3.

D. I(1; –2; –1), R = 9.

B - TỰ LUẬN

5,40. Trong không gian Oxyz, cho ba điểm A(1; 0; −1), B(0; 1; 2), C(−1; –2; 3).

a) Viết phương trình mặt phẳng (ABC).

b) Viết phương trình đường thẳng AC.

c) Viết phương trình mặt cầu đường kính AC.

d) Viết phương trình mặt cầu có tâm A và đi qua B.

5.41. Trong không gian Oxyz, cho đường thẳng d: 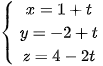. Viết phương trình mặt phẳng (P) chứa đường thẳng d và gốc toạ độ O.

5.42. Trong không gian Oxyz, cho mặt phẳng (P): x − 2y + 2z − 1 = 0 và hai điểm A(1; –1; 2), B(–1; 1; 0).

a) Tính khoảng cách từ A đến mặt phẳng (P).

b) Viết phương trình mặt phẳng (Q) đi qua A và song song với mặt phẳng (P).

c) Viết phương trình mặt phẳng (R) chứa A, B và vuông góc với mặt phẳng (P).

5.43. Trong không gian Oxyz, cho điểm A(1; 0; 2) và hai đường thẳng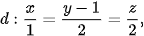

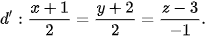
a) Xét vị trí tương đối của hai đường thẳng d và d'.

b) Viết phương trình đường thẳng Δ đi qua A và song song với đường thẳng d.

c) Viết phương trình mặt phẳng (P) chứa A và d.

d) Tìm giao điểm của đường thẳng d với mặt phẳng (Oxz).

5.44. Trong không gian Oxyz, cho mặt phẳng (P): x – 2y – 2z – 3 = 0 và đường thẳng 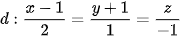. Viết phương trình mặt phẳng (Q) chứa d và vuông góc với mặt phẳng (P).

(Trang 63)

5.45. Trong không gian Oxyz, cho hai đường thẳng:

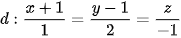và .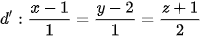

Viết phương trình mặt phẳng (P) chứa đường thẳng d và song song với đường thẳng d'.

5.46. Trong không gian Oxyz, cho hai mặt phẳng (P): x − y − z − 1 = 0, (Q): 2x + y − z − 2 = 0 và điểm A(−1; 2; 0). Viết phương trình mặt phẳng (R) đi qua điểm A đồng thời vuông góc với cả hai mặt phẳng (P) và (Q).

5.47. Trong không gian Oxyz, cho hai đường thẳng 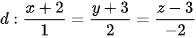và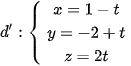

a) Xác định vị trí tương đối của hai đường thẳng d và d'.

b) Tính góc giữa d và d'.

5.48. Trong không gian Oxyz, tính góc tạo bởi đường thẳng 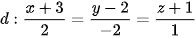và mặt phẳng (P): x + y – 2z + 3 = 0.

5.49. Trong không gian Oxyz, tính góc giữa mặt phẳng (P): x + y + z − 1 = 0 và mặt phẳng Oxy.

5.50. Từ mặt nước trong một bể nước, tại ba vị trí đôi một cách nhau 2 m, người ta lần lượt thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài 4 m; 4,4 m; 4,8 m. Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?

5.51. Bản vẽ thiết kế của một công trình được vẽ trong một hệ trục toạ độ Oxyz. Sàn nhà của công trình thuộc mặt phẳng Oxy, đường ống thoát nước thẳng và đi qua hai điểm A(1; 2; −1) và B(5; 6; −2). Tính góc tạo bởi đường ống thoát nước và mặt sàn.

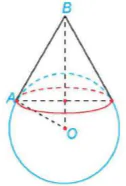
5.52. Nếu đứng trước biển và nhìn ra xa, người ta sẽ thấy một đường giao giữa mặt biển và bầu trời, đó là đường chân trời đối với người quan sát (H.5.45a). Về mặt Vật lí, đường chân trời là đường giới hạn phần Trái Đất mà người quan sát có thể nhìn thấy được (phần còn lại bị chính Trái Đất che khuất). Ta có thể hình dung rằng, nếu người quan sát ở tại đỉnh của một chiếc nón và Trái Đất được “thả” vào trong chiếc nón đó, thì đường chân trời trong trường hợp này là đường chạm giữa Trái Đất và chiếc nón (H.5.45b). Trong mô hình toán học, đường chân trời đối với người quan sát tại vị trí B là tập hợp những điểm A nằm trên bề mặt Trái Đất sao cho 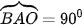, với O là tâm Trái Đất (H.5.45c). Trong không gian Oxyz, giả sử bề mặt Trái Đất (S) có phương trình 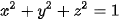và người quan sát ở vị trí B(1;1;–1).

Gọi A là một vị trí bất kì trên đường chân trời đối với người quan sát ở vị trí B. Tính khoảng cách AB.

Hình 5.45