Nội Dung Chính
(Trang 50)
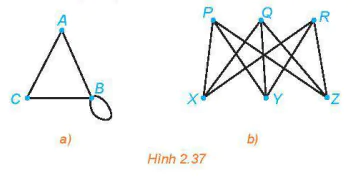
2.19. Viết tập hợp các đỉnh và tập hợp các cạnh của mỗi đồ thị sau:
2.20. Vẽ đồ thị G = (V, E) với các đỉnh và các cạnh như sau:
V= {1; 2; 3; 4; 5; 6; 7; 8} và E = {12; 13; 23; 34; 35; 67; 68; 78}.
Đồ thị này có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?
2.21. Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 6.
2.22. Chứng minh rằng nếu G là một đơn đồ thị có ít nhất hai đỉnh thì G có ít nhất hai đình có cùng bậc.
2.23. Tìm số đỉnh nhỏ nhất cần thiết để có thể xây dựng một đồ thị đầy đủ với ít nhất 1000 cạnh.
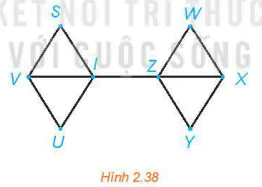
2.24. Hãy chỉ ra ít nhất 5 đường đi từ S đến Y trong đồ thị trên Hình 2.38.
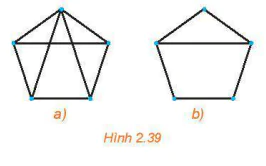
2.25. Kiểm tra xem các điều kiện của định lí Ore có thoả mãn với các đồ thị trên Hình 2.39 không.
(Trang 51)
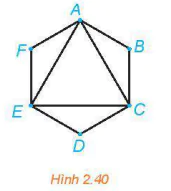
2.26. Tim một chu trình Euler trong đồ thị trên Hình 2.40.
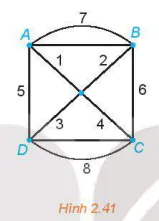
2.27. Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.41.
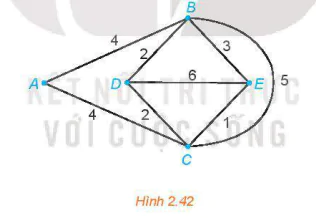
2.28. Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.42.
Các Bài Học Khác
Chuyên đề học tập Toán 11 - Bài 10: Bài Toán Tìm Đường Đi Tối Ưu Trong Một Vài Trường Hợp Đơn Giản - Tìm hiểu các phương pháp xác định đường đi ngắn nhất hoặc hiệu quả nhất trong những đồ thị đơn giản.
Xem thêm ⟶
Chuyên đề học tập Toán 11 - Bài 9: Đường Đi Euler Và Đường Đi Hamilton - Giới thiệu hai loại đường đi cơ bản trong lí thuyết đồ thị, giúp nhận diện và ứng dụng.
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn