Nội Dung Chính
(Trang 30)
| THUẬT NGỮ
| KIẾN THỨC, KĨ NĂNG
|
| Phép dời hình cho phép ta thể hiện mối quan hệ giống nhau cả về hình dạng và kích thước giữa các hình. Đối với các hình chỉ giống nhau về hình dạng mà khác nhau về kích thước thì sao? Đối tượng toán học nào cho phép ta thể hiện điều đó? |  |
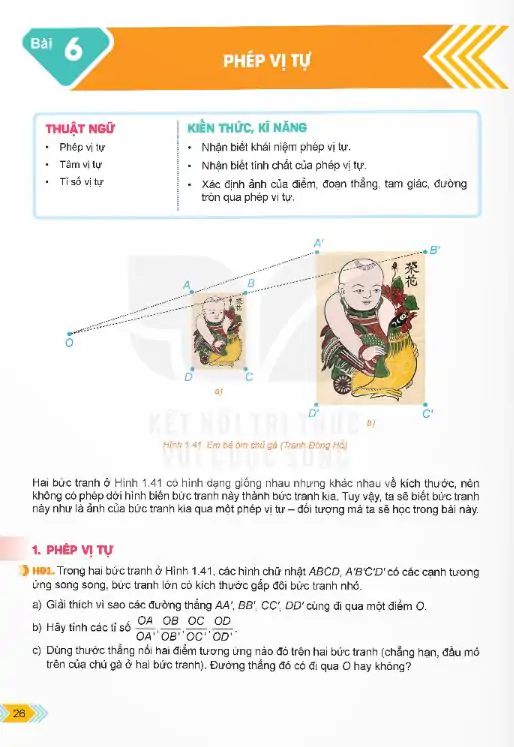
>HĐ. Hai tấm ảnh hình Dinh Thống Nhất ở hình trên giống nhau về hình dạng, chỉ khác nhau về kích thước.
a) Hãy đo và cho biết chiều dài, chiều rộng của tấm ảnh lớn tương ứng gấp mấy lần chiều dài, chiều rộng của tấm ảnh nhỏ.
b) Nếu hai vị trí A, B bất kì thuộc tấm ảnh nhỏ và các vị trí A′, B′ tương ứng với chúng trên tấm ảnh lớn thì khoảng cách giữa A′ và B′ gấp mấy lần khoảng cách giữa A và B? Hãy lấy ví dụ cụ thể các vị trí và đo để kiểm tra câu trả lời của bạn.
| Phép biến hình f được gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N và hai ảnh M', N' tương ứng của chúng, ta có M'N' = kMN. |
? Phép dời hình và phép vị tự tỉ số t có phải là các phép đồng dạng hay không? Nếu có thì có tỉ số đồng dạng là bao nhiêu?
>Ví dụ 1. Chứng minh rằng phép biến hình có được bằng cách thực hiện liên tiếp phép dời hình f và một phép vị tự V(O,k) là một phép đồng dạng với tỉ số 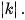
Giải
Với hai điểm bất kì M, N, giả sử phép dời hình f biến M, N tương ứng thành M', N' và V(O,k) biến M, N' tương ứng thành M", N". Vì f là phép dời hình nên MN = M'N'. Mặt khác
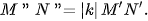
Do đó 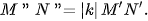 Vậy ta có điều phải chứng minh.
Vậy ta có điều phải chứng minh.
>Luyện tập 1. Chứng minh rằng phép biến hình có được bằng cách thực hiện liên tiếp phép đồng dạng f với tỉ số k1 và phép đồng dạng g với ti số k2 là một phép đồng dạng với ti số k1·k2.
(Trang 31)
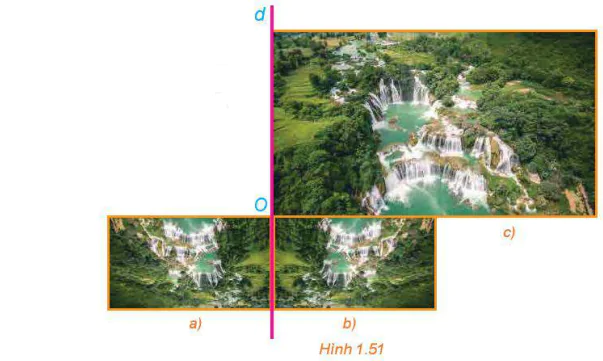
>Ví dụ 2. Trong Hình 1.51, Hình c) có kích thước gấp đôi các Hình a), b). Bằng quan sát, hãy chỉ ra phép đồng dạng biến Hình b) thành Hình c).
Giải
Phép đối xứng qua trục ở biến Hình b) thành Hình a). Phép vị tự tâm O, tỉ số –2 biến Hình a) thành Hình c). Như vậy, phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng trục ở và phép vị tự V(O;-2) biến Hình b) thành Hình c).
Chú ý. Với hai hình ![]()
>Luyện tập 2. Cho đường thẳng d và hai điểm A, B. Điểm M thay đổi trên đường thẳng d. Gọi N là điểm đối xứng của M qua đường thẳng AB và P là trung điểm của đoạn thẳng BN. Chứng minh rằng P thuộc một đường thẳng cố định.
>Vận dụng. Trong hai hình Dinh Thống Nhất ở Hình 1.50, hãy chỉ ra phép đồng dạng biến hình nhỏ thành hình lớn.
BÀI TẬP
1.24. Một phép đồng dạng biến ba đỉnh A, B, C của tam giác ABC tương ứng thành A', B', C'. Chứng minh rằng
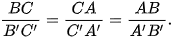
1.25. Trong mặt phẳng toạ độ Oxy, cho phép biến hình f biến mỗi điểm M(x; y) thành điểm M'(3x; -3y).
a) Tìm ảnh của các điểm O(0; 0), N(2; 1).
b) Chứng minh rằng f là một phép đồng dạng. Tìm tỉ số đồng dạng.
1.26. Hai hình và và   thành hình thành hình  . . | 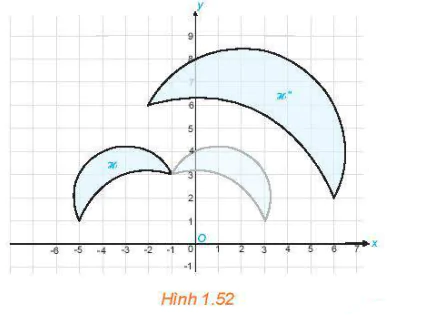 |
(Trang 32)
| Em có biết?
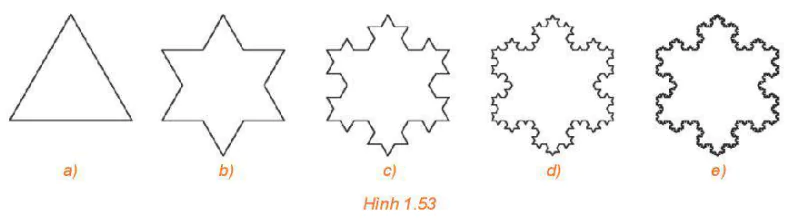
Ta bắt đầu với một hình tam giác đều (Hình a)). Chia mỗi cạnh của tam giác đó thành 3 đoạn thằng có độ dài bằng nhau và vẽ một tam giác đều nhận đoạn ở giữa làm cạnh đồng thời bỏ đi đoạn ở giữa đó, ta được Hình b). Tiếp tục chia mỗi cạnh của Hình b) thành 3 đoạn thằng có độ dài bằng nhau và vẽ một tam tam giác đều nhận đoạn ở giữa làm cạnh đồng thời bỏ đi đoạn ở giữa đó, ta được Hình c). Lặp lại quá trình trên, từ Hình c) ta tạo nên Hình d), từ Hình d), ta tạo nên Hình e), và cứ thế, ta sẽ được một dãy các hình, được gọi là dãy hình bông tuyết Koch (được đặt theo tên nhà toán học người Thuy Điển, Helge von Koch). Ta hoàn toàn có thể chứng minh được rằng, nếu tam giác đều ban đầu có cạnh là a thì bông tuyết Koch thứ n có chu vi là 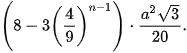 “Giới hạn” của dãy bông tuyết trên (khi n tiến ra vô tận) được gọi là bông tuyết Knock. Như vậy, bông tuyết Koch có chu vi bằng vô tận “Giới hạn” của dãy bông tuyết trên (khi n tiến ra vô tận) được gọi là bông tuyết Knock. Như vậy, bông tuyết Koch có chu vi bằng vô tận 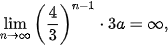 nhưng có diện tích hữu hạn và bằng nhưng có diện tích hữu hạn và bằng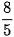 lần diện tích tam giác đều ban đầu lần diện tích tam giác đều ban đầu 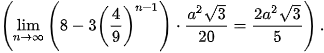 Mặc dù trong quá trình trên chúng ta chỉ tuân theo một quy tắc và lặp đi lặp lại nhiều lần, nhưng sau một số bước ta sẽ nhận được những hình trông khác xa so với hình ban đầu. Hình được tạo thành từ một hình cơ bản sau một quá trình lặp đi lặp lại một quy tắc được gọi là hình fractal. Bằng máy tính người ta dễ dàng tạo nên các hình fractal. Các cấu trúc fractal cũng phồ biến trong tự nhiên. Điều đáng lưu ý ở đây là mặc dù cấu trúc ban đầu có thể rất đơn giản nhưng sau một số bước đã tạo nên những cấu trúc phức tạp đến đáng kinh ngạc. Mặc khác, vì theo một quy tắc và lặp đi lặp lại nhiều lần, nên cấu trúc fractal cho ta hình ảnh mang tính tự đồng dạng như cây đồng dạng với cành cây.
|
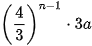







































































Bình Luận
Để Lại Bình Luận Của Bạn