(Trang 81)
SAU BÀI HỌC NÀY EM SẼ
- Sử dụng Excel phân tích được dữ liệu về tương quan tuyến tính ở mức đơn giản trong một bài toán thực tế.
- Trong thống kê và toán học, tương quan hoặc phụ thuộc là khái niệm được dùng để chỉ mối quan hệ giữa hai đại lượng biến đổi. Chẳng hạn, trong trường em bạn có chiều cao lớn hơn thường cũng có cân nặng lớn hơn. Hãy nêu vài ví dụ tương tự mà em biết.
1. TƯƠNG QUAN VÀ TƯƠNG QUAN TUYẾN TÍNH
Hoạt động 1 Tìm hiểu vai trò của phân tích tương quan
Phân tích tương quan đóng vai trò quan trọng trong việc đưa ra các quyết định ở nhiều lĩnh vực của kinh tế - xã hội. Nó cung cấp thông tin về mối quan hệ giữa các đại lượng biến đổi giúp nhận biết xu hướng và mức độ của mối quan hệ này. Chẳng hạn, thông tin về quan hệ giữa doanh số bán hàng và chi phí quảng cáo, giúp đánh giá hiệu quả của chiến lược quảng cáo và dự đoán mức tăng trưởng doanh số bán hàng. Em hãy cho biết:
a) Một số tình huống trong các lĩnh vực kinh tế - xã hội cần đến các phân tích này?
b) Làm thế nào để nhận biết xu hướng và mức độ tương quan tuyến tính của hai đại lượng biến đổi?
a) Tương quan giữa hai đại lượng biến đổi
Phân tích tương quan đóng vai trò quan trọng trong thống kê và nghiên cứu khoa học vì nó cung cấp thông tin về mối quan hệ giữa các biến. Điều này giúp nhận biết mô hình và xu hướng chung của dữ liệu, có thể cung cấp các thông tin hữu ích trong dự đoán và lập kế hoạch, giúp kiểm tra các giả định quan trọng của các mô hình thống kê.
Trong nghiên cứu kinh tế, phân tích tương quan có thể được sử dụng để xem xét mối quan hệ giữa các biến số như GDP (sản phẩm quốc nội) và tỉ lệ thất nghiệp. Mối tương quan giữa hai biến này có thể giúp dự đoán tác động của tăng trưởng kinh tế lên thị trường lao động.
Trong y tế, phân tích tương quan có thể được sử dụng để xác định mối quan hệ giữa các yếu tố rủi ro như hút thuốc lá, chế độ dinh dưỡng và tần suất mắc một số bệnh cụ thể.
Trong nghiên cứu xã hội học, phân tích tương quan có thể được sử dụng để đo lường mối quan hệ giữa giáo dục và thu nhập. Nếu có một tương quan tích cực, điều này có thể cho thấy rằng người có trình độ giáo dục cao thường có thu nhập cao hơn,...
(Trang 82)
Có nhiều dạng tương quan giữa hai đại lượng biến đổi (thể hiện qua quan hệ tương quan giữa hai dãy số liệu tương ứng), trong đó tương quan tuyến tính là đơn giản nhất. Tương quan tuyến tính (Linear Correlation) là mối quan hệ tuyến tính giữa hai biến số, khi một biến tăng/giảm 1 đơn vị thì biến kia cũng thay đổi xấp xỉ một lượng không đổi nào đó. Chẳng hạn, khi thu nhập của hộ tăng/giảm 1 triệu đồng thì chỉ tiêu tăng/giảm xấp xỉ 0.2 triệu đồng.
b) Hệ số tương quan tuyến tính
Trong thống kê, mẫu số liệu của hai biến X, Y là hai dãy số liệu tương ứng tạo thành các cặp số (X, Y), i = 1,..., n với n là số quan sát. Trong đó, dãy số X (i = 1,..., n) chứa các số liệu của biến X, dãy số Y, (i = 1,..., n) chứa các số liệu của biển Y. Chẳng hạn, trong Hình 11.1, hai biến điểm Toán và điểm Hoá học của 24 sinh viên là các cặp số liệu với số quan sát n = 24. Điểm Toán và điểm Hoá học của sinh viên thứ i kí hiệu là (X, Y) (i = 1,..., 24). Ví dụ, sinh viên thứ hai (mã hồ sơ 4548) có (X, Y) = (8.40, 3.25). Hình 14.1 mô tả một cách trực quan tương quan tuyến tính của Tổng điểm và điểm Hoá học nêu trong số liệu Hình 11.1: các điểm biểu diễn các cặp số liệu tương ứng phân bố "dọc theo" một đường thẳng xác định. 29 25 23 21 19 17 15
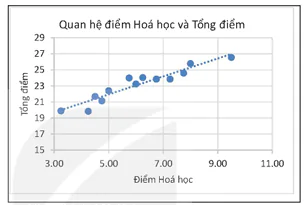
Hình 14.1. Mô tả trực quan tương quan tuyến tính trên đồ thị rải điểm
Để đo lường tương quan tuyến tính của hai biến X, Y người ta sử dụng hệ số tương quan tuyến tính (hay đơn giản là hệ số tương quan), kí hiệu là R(X, Y). Hệ số R(X, Y) có tính đối xứng, tức là R(X, Y) = R(Y, X).
Hệ số tương quan R(Y, X) thể hiện tương quan tuyến tính của hai biến X và Y ở hai khía cạnh:
- Chiều tương quan
| R(X,Y) > 0 | Tương quan dương (cùng chiều), cùng tăng hoặc cùng giảm |
| R(X,Y) < 0 | Tương quan âm (ngược chiều), biến này tăng biến kia giảm |
- Mức độ tương quan: Mức độ tương quan (mạnh, yêu) được đánh giá qua độ lớn của hệ số tương quan. Nếu |R(X,Y)] > [R(X,Z)| có thể nói rằng X và Y có tương quan tuyến tính mạnh hơn X và Z.
Khi phân tích tương quan tuyến tính, tuỳ thuộc lĩnh vực nghiên cứu người ta phân lớp độ mạnh yếu của quan hệ tương quan tuyến tính theo độ lớn của hệ số tương quan. Các nhà thống kê thường phân lớp mạnh yếu theo độ lớn của R(X,Y) như sau:
| IR(X,Y)| | < 0,3 | [0,3, 0,5) | [0,5; 0,7) | [0,7; 0,9) | ≥ 0,9 |
| Mức độ | Rất yếu | Yếu | Trung bình | Mạnh | Rất mạnh |
Các phần mêm bảng tính cung cấp các công cụ giúp tính hệ số tương quan R(X,Y) của hai biến X,Y từ dữ liệu quan sát được tổ chức thành hai dây số. Excel cung cấp hàm CORREL để tính giá trị R(X,Y).
- Hàm CORREL trả về hệ số tương quan tuyến tính của hai dãy số X và Y
Cú pháp: CORREL(array1, array2), trong đó:
array1, array2 là hai dãy số X và Y
(Trang 83)
Chú ý: Số liệu các hai biến khi tính hệ số tương quan phải là số liệu quan sát theo cặp dạng (X, Y), i = 1,...,n (n là số quan sát). Thông thường số cặp giá trị quan sát khác nhau tối thiểu là 5.
- Hai đại lượng biến đổi X,Y có thể có mối quan hệ tương quan tuyến tính. Hệ số tương quan tuyến tính dùng để đo lường mối quan hệ này.
- Hàm CORREL trong Excel dùng để tính Hệ số tương quan tuyến tính từ mẫu số liệu quan sát của X và Y.
1. Hệ số tương quan tuyến tính của hai biến X, Y dương cho biết điều gì?
2. Khi khai báo số liệu hàm CORREL tính R(X,Y) có cần chú ý đến thứ tự hai dãy số không?
2. THỰC HÀNH
Nhiệm vụ 1. Phân tích tương quan kết quả tuyển sinh
Yêu cầu: Theo kết quả tuyển sinh ở Hình 11.1, có ý kiến cho rằng nếu một sinh viên có điểm môn Toán cao thì Tổng điểm thi tốt nghiệp THPT cũng cao, tức là tương quan thuận chiều? Nhận định này có đúng không?
Hướng dẫn: Để tìm cơ sở cho nhận định trên, cần xác định hệ số tương quan tuyến tính của Tổng điểm với điểm Toán.
Bước 1. Mở trang Excel có nội dung như Hình 11.1. Tạo tiêu đề cho các ô R1:S1 và R2 như Hình 14.2.
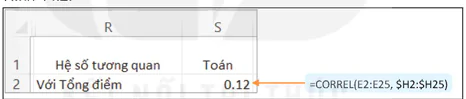
Hình 14.2. Hệ số tương quan tuyến tính giữa điểm thi môn Toán và Tổng điểm
Bước 2. Nhập =CORREL (E2:E25, SH2:$H25) vào ô S2.
Nhận xét: Kết quả cho thấy các hệ số tương quan tuyến tính của điểm Toán với Tổng điểm là 0.12 (lớn hơn 0), như vậy là tương quan thuận chiều. Nhưng hệ số tương quan là 0.12 cho thấy mức độ tương quan giữa Tổng điểm và điểm Toán quá yếu, có nghĩa là sẽ có sinh viên điểm Toán cao nhưng Tổng điểm không cao. Do vậy, nhận định trên là không luôn đúng.
Nhiệm vụ 2. Đánh giá mức độ tương quan
Yêu cầu: Theo kết quả tuyển sinh ở Hình 11.1, trong các môn Toán, Vật lí, Hoá học điểm thi môn nào có ảnh hưởng rõ nhất tới Tổng điểm theo nghĩa nếu điểm thi môn đó cao thì Tổng điểm nói chung cũng cao?
Hướng dẫn: Để tìm được câu trả lời, cần xác định hệ số tương quan tuyến tính của Tổng điểm với các môn thi.
Bước 1. Mở trang Excel có nội dung như Hình 11.1. Tạo tiêu đề cho các ô R1:U1 và R2 như Hình 14.3
Bước 2. Nhập công thức =CORREL (E2:E25, $H2:SH25) vào ô S2. Sao chép công thức ở ô S2 vào các ô T2:U2 để nhận kết quả như Hình 14.3.
(Trang 84)
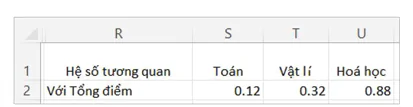
Hình 14.3. Trang số liệu và kết quả tính hệ số tương quan
Nhận xét: Hệ số tương quan tuyến tính giữa điểm môn Vật lí và Tổng điểm là 0.32, tuy có mạnh hơn so với môn Toán song vẫn ở mức yếu. Hệ số tương quan tuyến tính giữa môn Hoá học và Tổng điểm là 0.88 thể hiện mức độ tương quan mạnh. Điều đó có nghĩa là, nếu điểm thi môn Hoá học cao thì nói chung Tổng điểm thi cả ba môn Toán, Vật lí và Hoá học nói chung cũng ở mức cao. Nói cách khác, điểm thi môn Hoá học có ảnh hưởng tới Tổng điểm rõ hơn so với hai môn còn lại.
LUYỆN TẬP
1. Dùng số liệu ở Hình 11.1, hãy đánh giá mức độ tương quan giữa điểm Toán và điểm Vật lí, điểm Toán và điểm Hoá học.
2. Tính hệ số tương quan tuyến tính giữa chiều cao và cân nặng của nam, 18 tuổi với các số liệu sau:
| Chiều cao (cm) | 168 | 168 | 168 | 168 | 172 | 172 | 172 | 176 | 176 | 176 | 176 | 176 |
| Cân nặng (kg) | 57 | 57 | 57 | 57 | 64 | 64 | 64 | 68 | 68 | 68 | 68 | 68 |
VẬN DỤNG
1. Em hãy tính hệ số tương quan tuyến tính của dòng tiền đầu tư (V, đơn vị triệu đồng) và thời gian (t, đơn vị tháng) từ số liệu như bảng sau:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| V | 149,8 | 160,6 | 150,9 | 168,4 | 176,6 | 222,5 | 197,1 | 291.1 |
| t | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| V | 238,8 | 241,9 | 378,2 | 366,7 | 324,3 | 398,7 | 389,9 |
Giá trị khoản tiền đầu tư theo thời gian
2. Số liệu doanh thu của các cơ sở lữ hành (DTLH, đơn vị tỉ VND) và lượng khách du lịch trong nước (KND), lượng khách nước ngoài (KNN) cho ở bảng sau:
Đơn vị: 1000 lượt người
| Năm | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
| DTLH | 18852 | 24820 | 27799 | 30444 | 32530 | 36111 | 40371 | 44669 | 1649 | 6596 |
| KND | 70085 | 77863 | 90571 | 102200 | 117037 | 132837 | 144683 | 162046 | 78083 | 48949 |
| KNN | 9594 | 9569 | 9869 | 11811 | 12697 | 13747 | 14957 | 17318 | 7213 | 2550 |
Tính hai hệ số tương quan tuyến tính R(DTLH, KND) và R(DTLH, KNN). Nêu một vài nhận xét có thể từ kết quả tính được.

































































Bình Luận
Để Lại Bình Luận Của Bạn