(Trang 54)
SAU BÀI HỌC NÀY EM SẼ:
- Sử dụng được các hàm tổ hợp (ví dụ: PERMUT, COMBIN, COMBINA,...) tính xác suất một biến cố theo xác suất cổ điển.
- Sử dụng được hàm BINOM.DIST tính xác suất biến ngẫu nhiên theo phân phối nhị thức trong một số bài toán đơn giản.
- Sử dụng được các hàm (ví dụ: RAND, RANDBETWEEN,...) chọn trực tiếp ngẫu nhiên một số dữ liệu từ mẫu dữ liệu cho trước.
Em hãy nhắc lại khái niệm xác suất theo định nghĩa cổ điển đã được học trong môn Toán.
1. TÍNH XÁC SUẤT VÀ CHỌN SỐ LIỆU NGẪU NHIÊN TRONG EXCEL
Hoạt động 1 Tính xác suất bằng các hàm trong Excel
Trong môn Toán, em đã biết có thể tính xác suất P(A) của biến cố A trong một số bài toán đơn giản nhờ các hàm tổ hợp. Hãy kể tên các hàm đó và cho ví dụ.
a) Cách tính xác suất và các hàm tổ hợp
Để tính xác suất P(A) của một biến cố A theo định nghĩa cổ điển, ta cần xác định hai giá trị:
1. Số kết quả đồng khả năng trong phép thử cho A là n(A).
2. Số kết quả thuận lợi trong phép thử cho A là m(A).
Khi đó, xác suất P(A) của A là: P(A) = 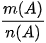
Trong nhiều trường hợp, có thể sử dụng các hàm tổ hợp để tính các giá trị n(A), m(A). Sau đây, em sẽ làm quen với một số hàm tổ hợp thường dùng trong phần mềm bảng tính Excel.
Một cách chọn có thứ tự k phần tử từ một tập hợp có n phần tử (1 ≤ k ≤ n) là một chỉnh hợp chập k của n. Hàm PERMUT được sử dụng để tính số các chỉnh hợp chập k của n.
Cú pháp: PERMUT(number, number_chosen), trong đó:
- number là số phần tử của tập hợp (n).
- number_chosen là số phần tử được chọn (k).
Ví dụ: Số cách chọn có thứ tự 3 học sinh từ nhóm có 10 học sinh cho 3 vị trí công việc khác nhau là số chỉnh hợp chập 3 của 10. Do vậy, có thể sử dụng công thức =PERMUT(10, 3) trong Excel để nhận được kết quả là 720.
(Trang 55)
- Một cách chọn k phần tử từ một tập hợp có n phần tử (1 ≤ k ≤ n) là một tổ hợp chập k của n. Hàm COMBIN được sử dụng để tính số các tổ hợp chập k của n.
Cú pháp: COMBIN(number, number_chosen), trong đó:
- number là số phần tử của tập hợp (n).
- number_chosen là số phần tử được chọn (k).
Ví dụ: Số cách chọn 3 học sinh, không phân biệt thứ tự, từ nhóm có 10 học sinh là số tổ hợp chập 3 của 10. Sử dụng công thức =COMBIN (10,3) trong Excel để nhận được kết quả là 120.
- Một cách chọn k phần tử từ tập hợp có n phần tử, k có thể lớn hơn n, các phần tử có thể chọn lặp lại và không tính đến thứ tự sắp xếp của chúng là một tổ hợp lặp chập k của n. Hàm COMBINA được sử dụng để tính số tổ hợp lặp chập k của n.
Cú pháp: COMBINA (number, number_chosen), trong đó:
- number là số phần tử của tập hợp (n).
- number_chosen là số phần tử được chọn (k).
Ví dụ 1: Số cách chọn học sinh để làm 3 việc trong nhóm 10 học sinh, một học sinh có thể được chọn làm nhiều việc, là số tổ hợp lặp chập 3 của 10. Ta có số cách lựa chọn =COMBINA (10, 3) bằng 220.
Ví dụ 2: Một tổ có 10 học sinh, trong giờ Tin học có 3 lần giáo viên yêu cầu giải thích công thức và mỗi lần gọi ngẫu nhiên 1 học sinh trong tổ theo hai cách:
a) Nếu không phân biệt học sinh đó đã được gọi hay chưa (có lặp). Số cách gọi này là =COMBINA(10,3) bằng 220.
b) Nếu lần sau không gọi học sinh đã được gọi trước đó (không lặp) thì số cách gọi là =COMBIN(10.3) bằng 120.
b) Xác suất biến ngẫu nhiên theo phân phối nhị thức
Phân phối nhị thức là phân phối xác suất của số lần xảy ra biến cố X (thử nghiệm thành công) trong một số lần thử nghiệm độc lập, trong đó mỗi thử nghiệm chỉ có hai kết quả có thể xảy ra (thành công hoặc thất bại). Có thể tính xác suất này bằng cách sử dụng hàm BINOM.DIST trong Excel.
Cú pháp: BINOM.DIST(number_s, trials, probability_s,cumulative), trong đó:
- number_s: số lần thử thành công (k).
- trials: số lần thử độc lập (n).
- probability_s: xác suất thành công trong mỗi lần thử (p).
- cumulative: tuỳ chọn (nếu cumulative bằng TRUE hay 1 thì hàm trả về xác suất số lần thành công nhỏ hơn hoặc bằng k, kí hiệu P(X≤k); nếu cumulative bằng FALSE hay 0 thì hàm trả về xác suất số thành công bằng k, kí hiệu P(X = k)).
Ví dụ: Một người bắn bia có xác suất mỗi lần trúng vòng 10 là 10% (p = 0.1), người đó bắn 20 lần (n = 20).
a) Công thức =BINOM.DIST(18, 20, 0.1, FALSE) cho kết quả là xác suất người đó bắn trúng vòng 10 đúng 18 lần (k = 18).
b) Công thức =BINOM.DIST(18, 20, 0.1, TRUE) cho kết quả là xác suất người đó bắn trúng vòng 10 nhiều nhất 18 lần (k = 18).
c) Chọn số liệu ngẫu nhiên
Trong nghiên cứu thống kê, việc chọn số liệu ngẫu nhiên rất cần thiết để đảm bảo tính đại diện và công bằng của mẫu đối với quần thể, làm giảm yếu tố chủ quan,
(Trang 56)
tăng khả năng tổng quát hoá kết quả và tính minh bạch của nghiên cứu. Ví dụ, trong kiểm định chất lượng sản phẩm, việc chọn ngẫu nhiên một số sản phẩm trong lô hàng để kiểm tra giúp đánh giá mẫu đại diện và đưa ra kết luận về chất lượng tổng thể của cả lô hàng. Trong Excel, các hàm sinh số ngẫu nhiên RAND và RANDBETWEEN có thể được dùng để hỗ trợ quá trình chọn số liệu ngẫu nhiên.
- Hàm RAND được sử dụng để sinh một số ngẫu nhiên trong nửa khoảng [0; 1).
Cú pháp: RAND(). Hàm này không có đối số.
- Hàm RANDBETWEEN được sử dụng để sinh một số nguyên ngẫu nhiên trong một đoạn xác định.
Cú pháp: RANDBETWEEN (bottom, top), trong đó:
- bottom là số nguyên nhỏ nhất mà hàm có thể trả về.
- top là số nguyên lớn nhất mà hàm có thể trả về.
Ví dụ: Công thức =RANDBETWEEN (1,3) trả về 1 hoặc 2 hoặc 3.
Lưu ý: Giá trị trả về của các hàm RAND và RANDBETWEEN thay đổi ngẫu nhiên khi có bất kì thay đổi nào trên trang tính. Vì vậy, nếu muốn cố định giá trị của các hàm này thì sau khi nhập hàm, ta nhấn phím F9 thay cho phím Enter.
d) Khai thác bảng chọn hàm trong Excel
Trong Excel, em có thể tạo công thức có hàm bằng cách mở bảng chọn Formulas chọn Insert Function hoặc nháy chuột chọn nút fx để mở hộp thoại Insert Function (Hình 10.1).
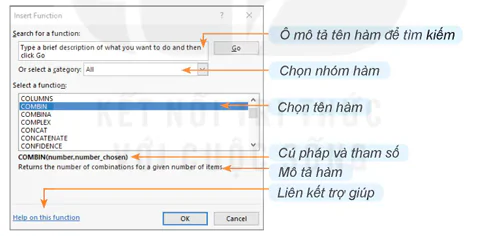
Ô mô tả tên hàm để tìm kiếm
Chọn nhóm hàm
Chọn tên hàm
Cú pháp và tham số
Mô tả hàm
Liên kết trợ giúp
Hình 10.1. Bảng chọn hàm
- Nếu biết tên hàm: Nhập tên hàm vào cửa sổ khai báo tên hàm Search for a function và chọn Go. Excel sẽ hiển thị tên hàm phù hợp trong danh sách Select a function.
- Nếu biết nhóm hàm chứa hàm cần tìm: Chọn nhóm hàm trong ô Or select a category.
- All: hiển thị tất cả các hàm.
- Math & Trig: có các hàm toán học như COMBIN, COMBINA, RAND, RANDBETWEEN.
- Nhóm Statistical: có các hàm thống kê như PERMUT, BINOM.DIST (Hình 10.2).
- Nháy đúp tên hàm trong danh sách Select a function để mở hộp thoại khai báo hàm (Hình 10.3).
(Trang 57)
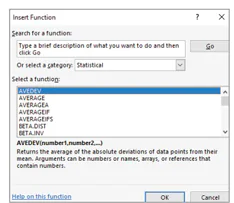
Hình 10.2. Nhóm hàm Statistical
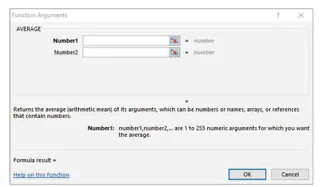
Hình 10.3. Hộp thoại khai báo hàm AVERAGE
Excel cung cấp các hàm tổ hợp như PERMUT, COMBIN, COMBINA; hàm tính xác suất đối với biến ngẫu nhiên theo phân phối nhị thức như BINOM.DIST, các hàm sinh số ngẫu nhiên như RAND, RANDBETWEEN.
1. Hàm nào sau đây không hỗ trợ tính xác suất theo định nghĩa cổ điển?
A. RAND
B. TỔNG HỢP
C. BINOM.DIST
D. CHO PHÉP
2. Đội thi tính nhanh trên máy tính cầm tay của lớp em có 4 người, nếu phải tính số cách chọn 2 người phụ trách nhóm thì em dùng hàm nào?
3. Hãy chọn hàm tạo ngẫu nhiên một số nguyên không nhỏ hơn 10 và không lớn hơn 15 trong các hàm sau:
A. RAND.
B. ĐƯỢC PHÉP.
C. RANDBETWEEN.
D. BINOM.DIST.
4. Em có 6 địa điểm tham quan A1...A6 yêu thích như nhau. Trong kì nghỉ hè, em dự định đi tham quan 3 lần, mỗi lần chọn ngẫu nhiên 1 địa điểm. Em sẽ dùng hàm nào để chọn địa điểm cho 3 lần tham quan:
a) Không chọn địa điểm đã tham quan?
b) Có thể chọn địa điểm đã tham quan?
2. THỰC HÀNH
Nhiệm vụ 1: Tính xác suất theo định nghĩa cổ điển
Yêu cầu: Sử dụng các hàm trong Excel để tính xác suất theo định nghĩa cổ điển trong một số bài toán đơn giản.
Nhiệm vụ 1.1. Một người muốn gọi điện thoại cho bạn nhưng quên mất 2 chữ số cuối cùng, chỉ nhớ đó là 2 chữ số khác nhau. Người đó bấm số với 2 chữ số cuối cùng ngẫu nhiên một lần nhưng không đúng số cần gọi. Em hãy giải thích tại sao.
Hướng dẫn:
Bước 1. Phân tích bài toán: Gọi A là biến cố "Bấm ngẫu nhiên 2 chữ số cuối cùng được đúng số cần gọi". Rõ ràng, chỉ có một cách bấm đúng 2 số cuối, vậy m(A) =1. n(A) là số cách bấm các số có 2 chữ số khác nhau trong 10 chữ số từ 0 đến 9. Có thể thấy, n(A) chính là số chỉnh hợp chập 2 của 10.
Bước 2. Tính xác suất của biến cố A trong Excel.
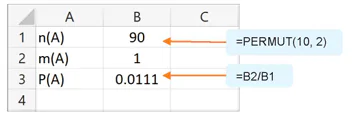
Nhập tiêu đề trang tính và các nhãn ở các ô của cột A như Hình 10.4.
Nhập = PERMUT(10,2) vào ô B1. Nhấn phím Enter được kết quả là 90.
(Trang 58)
Nhập giá trị 1 vào ô B2.
Nhập =B2/B1 vào ô B3. Nhấn Enter nhận kết quả là 0.0111 như Hình 10.4.
=PERMUT(10, 2)
=B2/B1
Hình 10.4. Tính xác suất bấm đúng số cần gọi
Kết quả trên cho thấy xác suất bấm ngẫu nhiên một lần 2 chữ số cuối đúng số cần gọi là 1.1%, tức là khả năng bấm chính xác ngay số điện thoại cần gọi có thể xem là gần như chắc chắn không xảy ra.
Nhiệm vụ 1.2. Đội tuyển cờ vua có 4 bạn lớp 10, 5 bạn lớp 11. Tính xác suất chọn ngẫu nhiên 3 bạn từ đội tuyển này, được 1 bạn lớp 10 và 2 bạn lớp 11.
Hướng dẫn:
Bước 1. Phân tích bài toán: Gọi biến cố cần tính xác suất “chọn ngẫu nhiên 3 bạn từ đội tuyển được 1 bạn lớp 10 và 2 bạn lớp 11” là A. n(A) là số cách chọn 3 bạn khác nhau từ 9 bạn, có nghĩa n(A) là số tổ hợp chập 3 của 9; m(A) là tích của số cách chọn 1 bạn trong 4 bạn lớp 10 (số tổ hợp chập 1 của 4) và 2 bạn trong 5 bạn lớp 11 (số tổ hợp chập 2 của 5).
Bước 2. Tính xác suất biến cố A trong Excel:
Nhập tiêu đề trang tính và nhãn ở cột A và dòng 2 như Hình 10.5.
Tính n(A): nhập công thức =COMBIN(B3, B4) vào ô B5, nhấn Enter.
- Tính m(A): nhập công thức =COMBIN(C3, C4)*COMBIN(D3, D4) vào ô B6, nhấn Enter.
- Nhập công thức =B6/B5 tính xác suất vào ô B7, nhấn Enter.
Kết quả nhận được P(A) = 47.6% (Hình 10.5).

Hình 10.5. Tính xác suất chọn được 1 bạn lớp 10 và 2 bạn lớp 11
Nhiệm vụ 1.3. Bạn Nam có hai đĩa nhạc yêu thích. Trong một tuần, Nam nghe nhạc bốn lần, mỗi lần chọn ngẫu nhiên một trong hai đĩa, không phân biệt đĩa đã nghe trong tuần hay chưa. Tính xác suất cả bốn lần chọn một đĩa.
Hướng dẫn:
Bước 1. Phân tích bài toán: Gọi A là biến cố cả bốn lần chọn đều chọn cùng một đĩa nhạc. n(A) là số cách chọn bốn lần từ hai đĩa nhạc. Ta có n(A) là số tổ hợp lặp chập 4 của 2.
(Trang 59)
(Trang 60)
(Trang 61)

































































Bình Luận
Để Lại Bình Luận Của Bạn