Nội Dung Chính
(Trang 6)
| Mặt Trời giữ các hành tinh quay xung quanh nó là do có trường hấp dẫn của Mặt Trời tác dụng lực hấp dẫn lên các hành tinh này. Vậy, trường hấp dẫn là gì? |  |
I. LỰC HẤP DẪN CỦA TRÁI ĐẤT
| Ném con là trò chơi dân gian vào các dịp lễ, Tết của một số đồng bào ở vùng núi phía Bắc nước ta (người chơi ném quả còn để nó có tốc độ ban đầu, sau đó buông tay ra để ném quả còn lên cao). Nếu quả còn bay qua hình tròn trên cây cọc thì người chơi giành chiến thắng. |
Hình 1.1. Trò chơi dân gian ném còn vào các dịp lễ, Tết. |
| ? Để ném được quả còn bay qua được hình tròn trên cây cọc thì người chơi phải ném xiên hay ném ngang quả còn? |
| Nêu ví dụ chứng tỏ tồn tại lực hấp dẫn của Trái Đất. |
II. LỰC HẤP DẪN
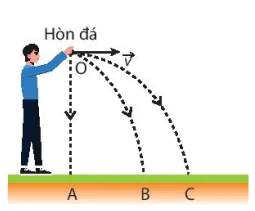
| Ở gần mặt đất, khi thả một viên đá thì nó sẽ rơi xuống mặt đất và khi ném viên đá ra xa thì nó cũng vẫn rơi xuống mặt đất (Hình 1.2).
|
Hình 1.2. Mô tả viên đá rơi khi thả và khi ném |
(Trang 7)
Nhà bác học Isaac Newton (I-xắc Niu-tơn) là người phát hiện ra lực làm cho viên đá rơi xuống mặt đất có cùng bản chất với lực giữ cho Mặt Trăng quay quanh Trái Đất và lực giữ cho các hành tinh quay quanh Mặt Trời.
Năm 1665, khi mới 23 tuổi, Isaac Newton đã khái quát: mọi vật trong vũ trụ đều hút nhau với một lực, gọi là lực hấp dẫn.
Dựa vào kết quả quan sát vị trí các hành tinh của Tikho Brahe (Ti-khô Bra-hê) (1546–1601), Johannes Kepler (Giô-han Kép-le) đã đưa ra ba định luật mô tả chuyển động của các hành tinh trong Hệ Mặt Trời.
Dựa vào quy luật chuyển động của các hành tinh trong Hệ Mặt Trời do nhà bác học Johannes Kepler tìm ra, Isaac Newton đã xác định được lực hấp dẫn và phát biểu như sau:
Hai vật tương tác lẫn nhau với một lực tỉ lệ nghịch với bình phương khoảng cách giữa chúng và tỉ lệ thuận với tích khối lượng hai vật.
Giả sử có hai vật là A và B, có khối lượng lần lượt là m1 và m2, cách nhau một khoảng r thì lực hấp dẫn giữa hai vật có độ lớn tỉ lệ với tích m1m2 và tỉ lệ nghịch với r2 (Hình 1.3).
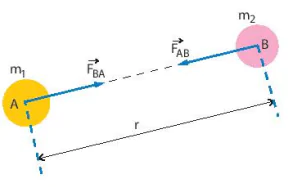
Hình 1.3. Biểu diễn lực hấp dẫn của vật A tác dụng lên vật B và vật B tác dụng lên vật A.
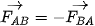
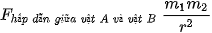
Thay dấu tỉ lệ bằng dấu bằng thì ta nhân thêm với hằng số G, khi đó biểu thức độ lớn của lực hấp dẫn là:
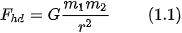
Trong đó m1, m2 có đơn vị là kilôgam (kg); r có đơn vị là mét (m) và Fhd có đơn vị là niutơn (N) thì hằng số G có đơn vị là 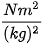 gọi là hằng số hấp dẫn.
gọi là hằng số hấp dẫn.
| ? Biểu thức 1.1 áp dụng trong điều kiện nào? |
| Nếu xác định được giá trị của G, biết được khối lượng của hai vật và khoảng cách giữa chúng thì có thể tính được độ lớn của lực hấp dẫn giữa hai vật đó theo biểu thức (1.1). Biểu thức (1.1) tính độ lớn của lực hấp dẫn chỉ đúng khi hai vật A, B là hình cầu có khối lượng phân bố đồng đều hoặc có bán kính rất nhỏ so với khoảng cách giữa hai vật. Khi đó, khối lượng của vật được xem như tập trung ở tâm của nó. |
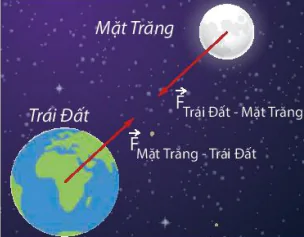
Hình 1.4. Lực tương tác giữa Mặt Trăng và Trái Đất có bản chất như lực tương tác giữa Trái Đất và viên đá trên Trái Đất. |
Mặt Trăng
Trái Đất
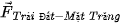
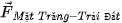
(Trang 8)
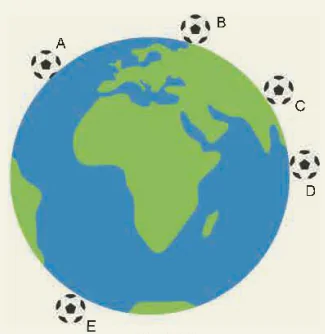
| 1. Biểu diễn lực hấp dẫn giữa Trái Đất và quả bóng trong các trường hợp quả bóng ở các vị trí khác nhau (Hình 1.5). 2. Nêu nhận xét về độ lớn, phương, chiều của lực hấp dẫn ở các vị trí trên? |
Hình 1.5. |
Giá trị của hằng số G do nhà bác học Cavendish (Ca-ven-đi-sơ) đo được chỉ sai khác khoảng 1% so với giá trị của G mà các thí nghiệm chính xác hơn sau này đo được là
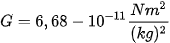
Hằng số hấp dẫn G có giá trị rất nhỏ, do đó lực hấp dẫn giữa các vật có khối lượng bình thường trong đời sống có giá trị vô cùng nhỏ, nên ta không cảm nhận được lực hấp dẫn giữa chúng.
| 1. Hãy biểu diễn lực hấp dẫn giữa quả táo đang rơi xuống mặt đất và Trái Đất. Tại sao ta không quan sát thấy Trái Đất rơi về phía quả táo? 2. Trình bày cách tính lực hấp dẫn giữa quả táo và Trái Đất khi biết khối lượng quả táo mà không áp dụng biểu thức 1.1. |
| 3. Nêu cách biểu diễn lực hấp dẫn giữa hai chất điểm. 4. Tính lực hấp dẫn giữa hai quả cầu giống nhau, khối lượng mỗi quả cầu là 3 kg, có bán kính 10 cm, tâm của hai quả cầu đặt cách nhau là 80 cm. So sánh lực hấp dẫn của hai quả cầu trên với trọng lực của chúng. Giải thích tại sao hai lực này lại có độ lớn khác nhau. |
Dựa vào lực hấp dẫn, các nhà thiên văn đã dự đoán các chu kì nhật thực, nguyệt thực và tìm được thêm các hành tinh chưa biết trong Hệ Mặt Trời.
(Trang 9)
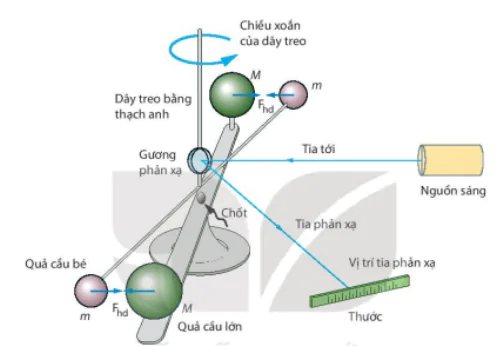
| EM CÓ BIẾT Hơn một thế kỉ sau khi phát hiện ra định luật hấp dẫn của Newton, nhà bác học Henry Cavendish mới tìm được độ lớn của hằng số hấp dẫn G bằng thí nghiệm gồm sợi dây thạch anh có gắn gương phản xạ và một thanh ngang có gắn hai quả cầu nhỏ giống nhau, đặt cạnh hai quả cầu lớn có khối lượng gần bằng 160 kg và bán kính 23 cm (Hình 1.6).
Hình 1.6. Mô hình mô tả nguyên tắc hoạt động của thí nghiệm đo hằng số hấp dẫn G của nhà bác học Cavendish (1731 – 1810). Khi chiếu ánh sáng vào gương sẽ thu được vị trí tia phản xạ trên thước, lực hấp dẫn xuất hiện giữa quả cầu lớn và quả cầu nhỏ sẽ làm quả cầu nhỏ dịch lại gần quả cầu lớn, dây treo bị xoắn lại, vị trí tia phản xạ sẽ thay đổi, từ đó tính được góc xoắn của dây treo và tính được giá trị của G. |
Chiều xoắn của dây treo
Dây treo bằng thạch anh
Gương phản xạ
Tia tới
Tia phản xạ
Quả cầu bé
Quả cầu lớn
Nguồn sáng
Vị trí tia phản xạ
Thước
III. TRƯỜNG HẤP DẪN
Các vật có khối lượng luôn tương tác hấp dẫn với nhau bằng lực hấp dẫn giữa chúng nên xung quanh vật có khối lượng có trường hấp dẫn.
Trường hấp dẫn của vật này sinh ra lực hấp dẫn tương tác lên vật khác đặt trong nó.
Ở lớp 10 chúng ta đã biết trên Trái Đất, mọi vật đều chịu tác dụng của trọng lực là lực hấp dẫn giữa vật và Trái Đất. Trọng lực là trường hợp riêng của lực hấp dẫn.
(Trang 10)
| Dựa vào các hiện tượng dưới đây, hãy thảo luận để chứng tỏ mọi vật có khối lượng đều tạo ra một trường hấp dẫn xung quanh nó. | ||
|
Hình 1.7. Vận động viên nhảy dù đang rơi. Nhảy dù là môn thể thao mạo hiểm mà vận động viên nhảy ra khỏi máy bay đang bay ở độ cao hàng nghìn mét. Khi vận động viên rời khỏi máy bay thì sẽ rơi xuống Trái Đất. |
Hình 1.8. Trạm vũ trụ quay quanh Trái Đất. Vệ tinh là vật quay quanh các hành tinh. Trong Hệ Mặt Trời, Thủy tinh, Kim tinh không có vệ tinh tự nhiên, Trái Đất chỉ có một vệ tinh là Mặt Trăng và rất nhiều vệ tinh nhân tạo do con người phóng lên. Trạm vũ trụ cũng là vệ tinh nhân tạo. |
Hình 1.9. Hệ Mặt Trời quay quanh Tâm Ngân Hà của chúng ta. Ngân Hà là hệ gồm nhiều ngôi sao và bụi quay quanh tâm của của nó. Tâm Ngân Hà có khối lượng vô cùng lớn. |
Trường hấp dẫn là trường lực được tạo ra bởi vật có khối lượng.
Trên Trái Đất, hiện tượng thuỷ triều là do sự tác động của trường hấp dẫn do Trái Đất, Mặt Trăng và Mặt Trời gây ra.
| 1. Nêu nhận xét vị trí của Mặt Trăng và Mặt Trời với Trái Đất khi có triều cường và triều thấp. 2. Dựa vào hiện tượng thuỷ triều lên xuống, hãy chứng tỏ trường hấp dẫn là dạng vật chất tồn tại quanh một vật có khối lượng và tác dụng lực hấp dẫn lên vật có khối lượng đặt trong nó. 3. Nêu tác động của triều cường đối với đời sống của người dân. |
| Trường hấp dẫn của các ngôi sao rất lớn có thể hút các đám bụi xoay quanh tạo thành các hành tinh chuyển động như Hệ Mặt Trời của chúng ta. Nếu hai ngôi sao ở gần nhau thì trường hấp dẫn của chúng sinh ra lực hút lẫn nhau, tạo thành cặp sao đôi. Hiện tượng sao đôi là một cặp ngôi sao luôn quay quanh nhau nhờ trường hấp dẫn của chúng. |
Hình 1.10. Cặp sao đôi Albiero trong chòm sao Thiên Nga. |
(Trang 11)
| Sao đôi rất quan trọng trong vật lí thiên văn, quan sát quỹ đạo của sao đôi giúp xác định khối lượng của chúng. Hãy tìm hiểu để nêu các cách phân loại sao đôi? |
Như vậy, trường hấp dẫn là dạng vật chất tồn tại quanh vật có khối lượng và tác dụng lực hấp dẫn lên vật có khối lượng đặt trong nó.
| EM CÓ BIẾT Hệ Mặt Trời của chúng ta đang quay quanh tâm Ngân Hà với tốc độ xấp xỉ 800 000 km/h, gấp hơn 7 lần tốc độ chuyển động của Trái Đất quanh Mặt Trời. Ngân Hà chứa Hệ Mặt Trời của chúng ta cùng đang quay quanh một Thiên Hà với chu kì khoảng 250 triệu năm. Tâm Ngân Hà là vật có khối lượng vô cùng lớn, tạo ra trường hấp dẫn rất lớn để Hệ Mặt Trời, các ngôi sao và bụi phải quay quanh nó, nhiều Thiên Hà của chúng ta cũng chỉ là một phần rất nhỏ của dải Thiên Hà. Trong vũ trụ, có đến hàng trăm tỉ Thiên Hà khác nhau. Tâm Thiên Hà là hố đen, là vật siêu khối lượng, tạo ra trường hấp dẫn mạnh tới mức hút hết cả ánh sáng vào trong hố đen, nên chúng ta không thể nhận được ánh sáng từ tâm Thiên Hà phát ra để quan sát chúng. |
Hình 1.11. Mô phỏng hố đen ở tâm Thiên Hà. |
IV. CHUYỂN ĐỘNG CỦA VẬT TRONG TRƯỜNG HẤP DẪN CỦA TRÁI ĐẤT
Năm 1687, trong cuốn sách “Những nguyên lí toán học của triết học tự nhiên” Newton đã trình bày thí nghiệm tưởng tượng về bắn viên đạn đại bác trên đỉnh núi với các vận tốc ban đầu khác nhau (Hình 1.12).
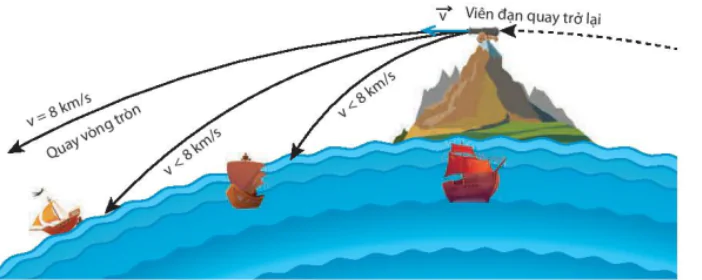
Hình 1.12.
v =8 km/s
Quay vòng tròn
v< 8 km/s
v<8 km/s
Viên đạn quay trở lại
(Trang 12)
| Giả sử nình núi trong thí nghiệm tưởng tượng của Niu-tơn có độ cao là 300 m, bán kính và khối lượng của Trái Đất lần lượt là 6 400 km và 6.1024 kg. Hãy xác định: 1. Gia tốc độ lực hấp dẫn của Trái Đất gây ra cho viên đạn bắn ra. 2. So sánh lực hấp dẫn của Trái Đất tác dụng lên viên đạn với lực hướng tâm của nó khi viên đạn chuyển động tròn? |
Chúng ta đã biết, khi vật rơi trên bề mặt Trái Đất mà chỉ chịu tác dụng của trọng lực thì nó sẽ rơi tự do.
Trọng lực tác dụng lên vật chính là lực hấp dẫn giữa Trái Đất và vật, có điểm đặt ở trọng tâm của vật.
Trọng lượng của vật là độ lớn lực hút của Trái Đất tác dụng lên vật.
Khi thả vật có khối lượng m ở độ cao h so với mặt đất, nếu lực cản không đáng kể thì vật sẽ rơi với gia tốc g.
Theo định luật II Newton ta có:
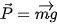
Lực này chính là lực hấp dẫn do tương tác giữa vật và Trái Đất, nên:
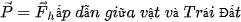
Suy ra: 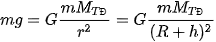
Trong đó, R và MTĐ lần lượt là bán kính và khối lượng của Trái Đất.
Ta có: 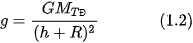
| Từ biểu thức (1.2) hãy chứng tỏ rằng, tại mỗi vị trí ở gần bề mặt của Trái Đất trong một phạm vi không lớn thì g là hằng số. Tính giá trị của g khi đó. |
Giá trị g0 = 9,81 m/s2 đã biết do đo được bằng thực nghiệm trong chuyển động rơi tự do của vật, từ đó ta có thể tính được khối lượng của Trái Đất theo biểu thức:
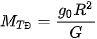
Do đó, thí nghiệm xác định hằng số hấp dẫn G của nhà bác học Cavendish còn được gọi là phép cân Trái Đất.
Từ biểu thức (1.2) ta rút ra được biểu thức gia tốc rơi tự do phụ thuộc độ cao như sau:
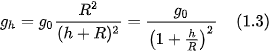
Từ biểu thức (1.3) cho thấy, càng lên cao thì gia tốc rơi tự do càng giảm.
(Trang 13)
| Tính gia tốc rơi tự do của vật ở các độ cao khác nhau như mô tả trong bảng sau:
|
| EM ĐÃ HỌC
|
| EM CÓ THỂ
|
(Trang 14)
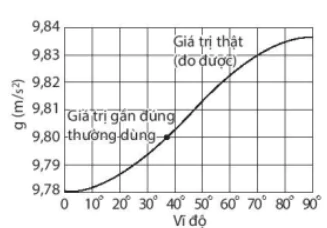
| EM CÓ BIẾT Giá trị độ lớn gia tốc rơi tự do g theo thấy đổi theo độ do sự phân bố khối lượng của Trái Đất là không đồng nhất và ảnh hưởng của sự tự quay quanh trục Bắc-Nam của nó. Giá trị của gia tốc rơi tự do thay đổi theo vị độ được mô tả như Hình 1.13. Biểu thức 1.1 được áp dụng trong trường hợp hai vật cách nhau cỡ như hai chất điểm hay hai vật có dạng hình cầu khối lượng phân bố đồng nhất. Đối với Trái Đất của chúng ta, có khối lượng phân bố không đồng nhất, có những vùng đất dương, đồi núi, dưới vỏ Trái Đất có thể có mỏ dầu, mỡ quang... nên trong lực củ chúng cũng đó sẽ thay đổi. Dựa vào các điểm này, các nhà khoa học đã tìm ra phương pháp thăm dò trong lực (Gravimetry) để nghiên cứu cấu trúc địa chất của vỏ Trái Đất. Ngày nay, người ta đã phát minh ra máy đo trọng lực với độ chính xác cao, có thể đặt trên đất liền, trên máy bay, tàu biển để đo những thay đổi này ở các cấu trúc địa chất gần đó, hoặc của bình dạng của Trái Đất, và do các biến động thuỷ triều dựa vào lực hấp dẫn (Hình 1.14). Từ đó, người ta xác định được bản đồ trọng lực của Trái Đất. |
Hình 1.13. Giá trị gia tốc rơi tự do ở gần mặt đất tại các vĩ độ khác nhau.
Hình 1.14. Máy đo trọng lực. |
Giá trị thật (đo được)
Giá trị gần đúng thường dùng














































































Bình Luận
Để Lại Bình Luận Của Bạn